💸 La règle des 72 : La formule magique que les banquiers ne t'expliquent jamais
#155, Comment calculer en 2 secondes le temps pour doubler ton capital — et pourquoi c’est l’outil le plus puissant pour comparer n’importe quel placement
Mes newsletters sont souvent longues, je vous invite à cliquer sur le bandeau pour lire l'intégralité directement sur Internet. De plus, merci de liker ou partager, cela va permettre de développer encore plus Cash Conseils. Petit sondage à la fin... N'oublie pas aussi de liker, ça m'aide à développer ❤️❤️❤️❤️Déjà 155 éditions de cette newsletter envoyée tous les dimanches
Vous aimez son contenu, je vous invite à cliquer sur le ♥️ au-dessus, ça m’aidera énormément.
On vous a transféré la news et vous voulez vous abonner ? 👇👇👇
Tu peux aussi me poser directement une question sur le sujet que tu veux…
🛎️ Ding Ding Ding, l’espace des liens
💶 Sponsoriser la newsletter : Pour vous adresser à ma communauté
🧑💻 Les réseaux : Linkedin, Youtube, Tiktok
🤝 Se retrouver : RDV, Newsletter, Youtube, tous les liens y sont
🤚 Rejoindre la communauté : sur Whatsapp
⚔️ Un coaching personnel : Prendre RDV
📖 Étude de mon patrimoine gratuite (diffusée…): Je veux que tu étudies mon patrimoine
Au sommaire cette semaine
🗞️ Finance Weekly : les cinq faits marquants de la semaine dernière
🧮 La formule en une phrase
🔍 Les 7 applications qui changent tout
📈 L’intérêt composé - la 8ème merveille du monde
✅ Ton plan d’action
Temps de lecture : 8 à 10 minutes selon ta vitesse de lecture
📈 Vous, mes abonnés : Nous sommes à 14 187 abonnés. Les abonnements remontent, si vous pouvez partager la newsletter autour de vous, ce serait top.
⚡ Linkedin : Suivez mes publications quotidiennes sur Linkedin. Des actualités fortes, du décryptage de tendances, tout y est. Voici pour me suivre
On me demande un peu de perso à chaque fois, de life style. Je peux vous dire plusieurs choses :
Cette semaine les enfants sont chez mes parents, ils sont en vacances, et nous …
Réunion entre associés sur Chatelaillon-Plage, on a bien avancé, et qu’est ce qu’on a bien mangé
Entrainement vendredi soir, sous la pluie, dans la boue, génial. Sauf pour le cycle de lavage, je ne trouve pas, “Plus de boue que de tissus”
Enky : investis dans du mobilier pro et génère jusqu’à 9% de rendement
Tu cherches un placement alternatif, concret et accessible ? Enky te permet de financer du mobilier professionnel loué à des entreprises comme Natixis, PayPlug ou le groupe BPCE.
Le principe est simple : des entreprises louent du mobilier haut de gamme (bureaux, hôtellerie, immobilier locatif), et toi tu finances ces projets dès 500€. En échange, tu perçois des revenus mensuels avec un rendement de 6 à 9%.
Depuis son lancement en avril 2024, Enky a déjà convaincu plus de 4 700 investisseurs et financé 12 millions d’euros de projets. Le tout sans aucun frais d’entrée ni de gestion.
Côté sécurité, Enky a mis en place des mesures de protection du capital : en cas de défaut d’un client, ils continuent de verser les intérêts et se chargent de relouer le mobilier.
Bonus Cash Conseils : 100 à 300€ offerts sur ton premier investissement via notre lien partenaire.
🔥 Plan P : Ta Semaine Finances 360° — C’est dans moins de 2 mois !
Du 13 au 18 avril 2026, rejoins le plus grand événement gratuit de France dédié à l’éducation financière.
Ce qui t’attend : 80 experts reconnus en live pendant 6 jours — psychologie financière, investissement, immobilier, fiscalité, entrepreneuriat et stratégie patrimoniale.
Les nouveautés :
→ La Banque de France participe officiellement à l’événement
→ Guillaume Martinaud, Président d’Orpi, rejoint le programme
→ Des influenceurs finance de premier plan : Joachim Savigny, Nicolas Pajot, Florent Albero, Yoann Lopez…
→ Couverture média en cours : Sud Radio, France TV, Europe 1, MoneyVox
Pourquoi c’est 100% gratuit ? Parce que l’éducation financière ne devrait pas être un luxe. L’événement est financé par nos partenaires.
👉 Inscris-toi maintenant — Plus de 1 500 personnes nous ont déjà rejoints.
👉 Intéressé(e) par le stage ? Écris moi
Bien que je sois le fondateur d’un cabinet en gestion de patrimoine, il est important de souligner que Cash Conseils 💸 opère indépendamment de cette entité. Cette newsletter s'inscrit dans une démarche entièrement dédiée à la pédagogie financière, visant à éduquer et à inspirer un large public sur les fondamentaux de la gestion financière personnelle. Cash Conseils 💸 est conçu pour être une ressource éducative ouverte à tous, sans liens directs avec les services ou les orientations spécifiques du cabinet. L'objectif est de fournir une plateforme neutre et informative, où chacun peut apprendre à naviguer dans l'univers des finances personnelles, en toute indépendance et sans conflit d'intérêts.
🚨 Kristi Noem sous pression : le DHS au bord du shutdown après les bavures de Minneapolis : La secrétaire à la Sécurité intérieure fait face à une tempête parfaite : le Congrès n’a pas voté le budget du DHS, menaçant de paralyser l’agence chargée des expulsions. Le Wall Street Journal révèle son “style d’autopromotion” — jets privés, pub personnelle après la mort de deux citoyens américains à Minneapolis. Tom Homan a repris les rênes des opérations au Minnesota et mis fin au déploiement massif d’agents, tandis que les Démocrates refusent tout financement supplémentaire à l’ICE.
💸 Amazon mise 200 milliards $ sur l’IA pour rattraper son retard sur Microsoft et Google : Face aux craintes internes qu’AWS ait “raté le boom de l’IA”, Andy Jassy lance le plus gros investissement de l’histoire d’Amazon — dépassant Google et Microsoft réunis. L’enjeu : reconquérir le terrain perdu face à OpenAI (contrat de 250 Mds $ avec Microsoft) avec ses puces Trainium, ses modèles Nova et son partenariat avec Anthropic (8 Mds $). Mais l’action a chuté de 20 % depuis novembre, et en interne certains craignent le “Jour 2“ redouté par Bezos — celui du “déclin inexorable”.
🇹🇼 TSMC : l’énigme des 250 milliards $ d’investissements US exigés par Trump : L’accord commercial US-Taïwan cache un deal colossal : TSMC devrait ajouter 100 milliards $ d’investissements à ses 165 Mds déjà annoncés, pour construire jusqu’à 10 usines en Arizona. En échange, Nvidia, Apple et les géants US obtiendraient des quotas d’importation sans droits de douane. Mais l’objectif de Lutnick — transférer 40 % de la production taïwanaise aux États-Unis — est jugé “impossible“ par Taipei, et personne ne sait encore comment taxer les puces intégrées dans les produits finis.
📱 Pakistan : le fisc traque les fraudeurs sur Instagram et les mariages fastueux : La “cellule de surveillance du train de vie“ du fisc pakistanais épluche les réseaux sociaux pour débusquer les riches contribuables déclarant des pertes. Exemple : une influenceuse de Lahore a organisé un mariage à 238 millions de roupies (850 000 $) tout en déclarant une perte de revenus de 2 700 $. Dans un pays où seulement 2 % de la population paie l’impôt sur le revenu et où l’industrie du mariage pèse 4 milliards $/an en cash, les critiques dénoncent un “gadget” qui évite de s’attaquer aux vrais fraudeurs — hauts fonctionnaires et militaires.
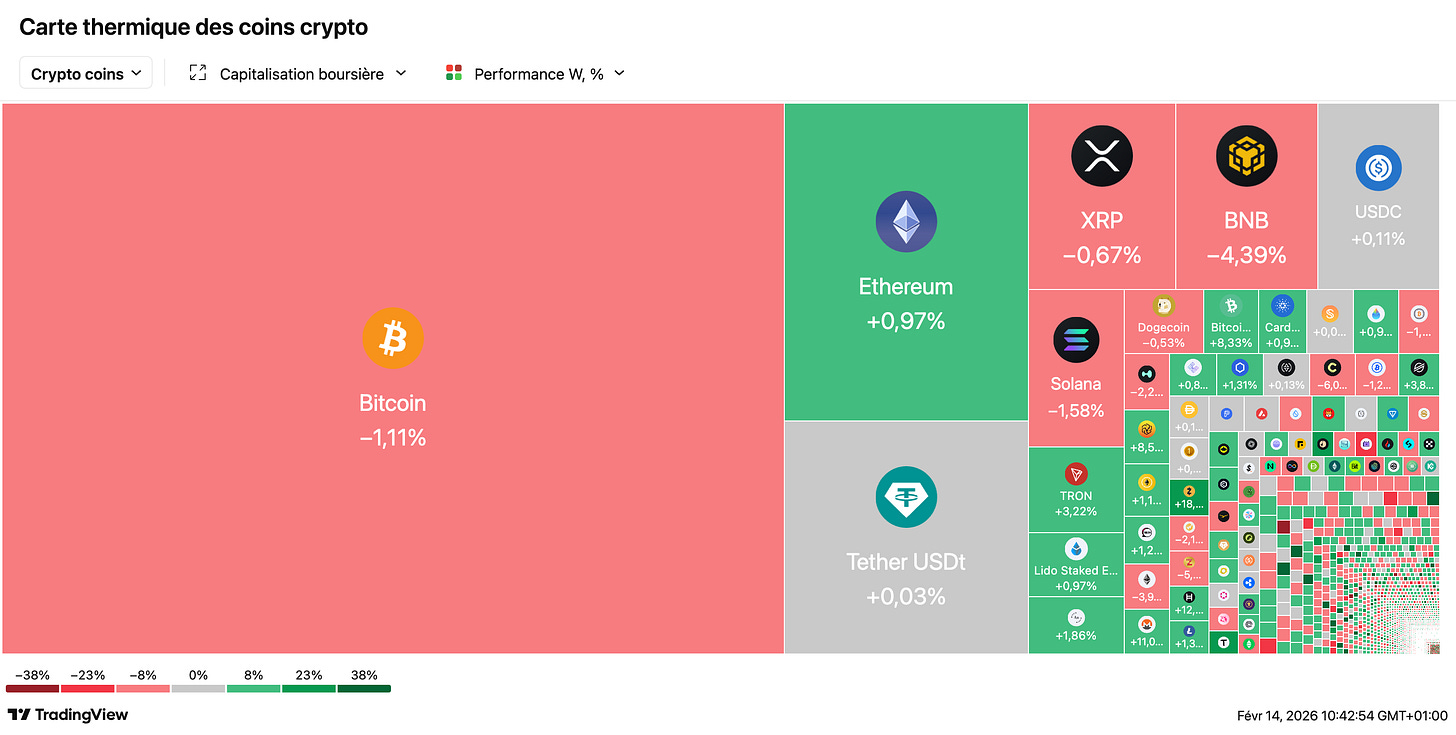
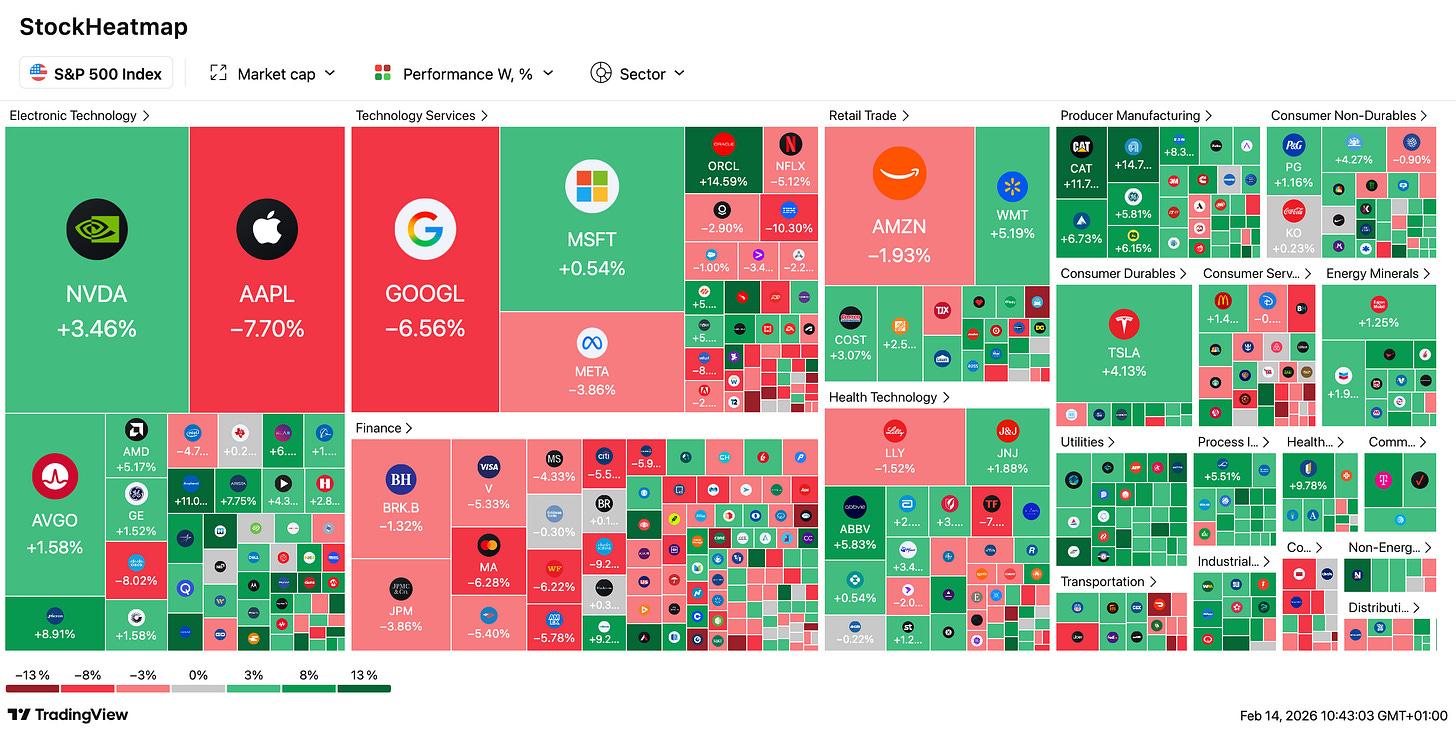
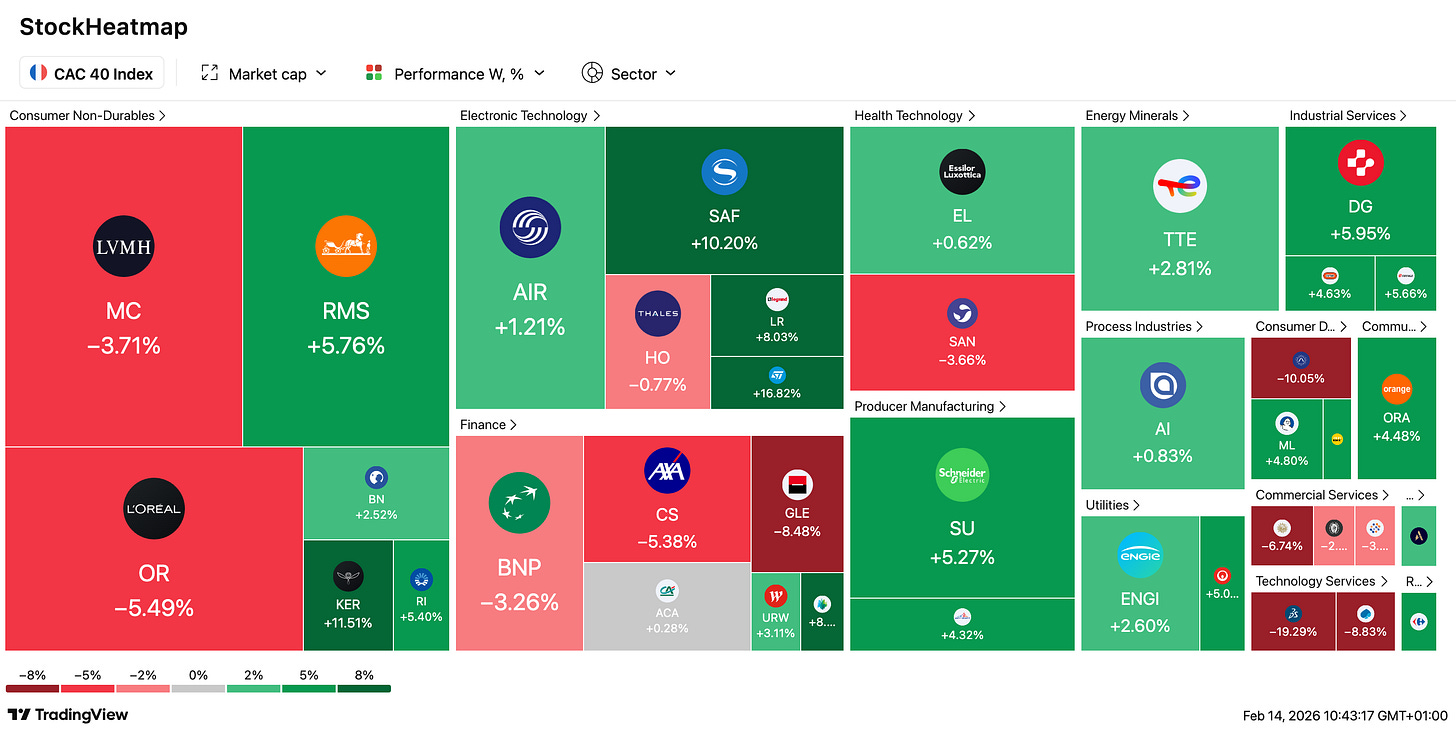
📈 CAC 40 : record historique en séance, inflation US rassurante, Safran s’envole : L’indice parisien gagne +0,46 % sur la semaine malgré un vendredi en repli, après avoir touché un plus haut historique à 8.437 points jeudi. Safran bondit de +8,3 % (record) sur d’excellents résultats 2025, Capgemini +5 % ; L’Oréal chute de -5 % sur un CA décevant. L’inflation US de janvier rassure (2,4 % annuel, sous les attentes), faisant tomber le 10 ans US sous 4,10 % — mais le CBO prévoit un déficit de 1.900 milliards $ cette année, alourdi par les tarifs douaniers qui pèsent à 95 % sur les entreprises et consommateurs américains.
Ton banquier connaît cette formule. Ton conseiller financier aussi. Les gérants de fonds d’investissement l’utilisent tous les jours. Les actuaires des compagnies d’assurance la maîtrisent sur le bout des doigts. Mais toi, personne ne te l’a jamais expliquée. Ni à l’école, ni au lycée, ni à la fac (sauf si tu as fait des études de finance). Et certainement pas dans les brochures commerciales des placements qu’on essaie de te vendre. Cette formule tient en une ligne, elle se calcule de tête en moins de deux secondes, et elle va changer ta façon de voir tous tes placements financiers. Elle s’appelle la règle des 72, et après avoir lu cette newsletter, tu ne pourras plus jamais regarder un taux de rendement de la même manière.
Pourquoi est-ce que je te parle de cette règle aujourd’hui ? Parce que la semaine dernière, j’ai eu une conversation édifiante avec un ami qui hésitait entre deux placements. Le premier lui promettait du 2 % par an, le second du 6 %. « C’est juste 4 points de différence », m’a-t-il dit, « ce n’est pas énorme ». Je lui ai alors posé une simple question : « Tu sais en combien de temps ton argent double dans chaque cas ? » Il a sorti sa calculatrice, tapé des formules pendant cinq minutes, et quand il a vu le résultat, il est resté bouche bée. Avec le placement à 2 %, son argent double en 36 ans. Avec le placement à 6 %, il double en 12 ans. Ce n’est pas « juste 4 points de différence ». C’est 24 années de ta vie d’écart. Et j’ai calculé ça de tête en deux secondes grâce à la règle des 72.
Dans cette newsletter, je vais t’apprendre cette formule magique et toutes ses applications pratiques. Tu vas découvrir comment comparer n’importe quels placements instantanément, comment mesurer ce que l’inflation te vole réellement, comment évaluer le vrai coût des frais bancaires, comment planifier ta retraite sur un coin de table, et même comment cette règle peut t’aider à négocier ton salaire. À la fin de cette lecture, tu auras un outil mental que tu utiliseras toute ta vie, et tu te demanderas comment tu as pu t’en passer jusqu’ici.
🧮 La formule en une phrase
La règle des 72 est d’une simplicité désarmante. Pour savoir en combien d’années ton capital va doubler à un taux de rendement donné, tu divises simplement 72 par ce taux. C’est tout. Pas besoin de calculatrice, pas besoin de tableur Excel, pas besoin de formules exponentielles compliquées. Juste une division de tête que tu peux faire pendant que ton banquier te vante les mérites de son dernier produit d’épargne.
Prenons des exemples concrets pour que tu visualises la puissance de cette formule. Le Livret A rapporte actuellement 2,4 % par an. Combien de temps pour doubler ton capital ? 72 divisé par 2,4 égale 30 ans. Si tu places 10 000 euros sur ton Livret A aujourd’hui, tu auras 20 000 euros dans 30 ans. Trente ans ! C’est une génération entière. C’est passer de 30 ans à 60 ans. C’est voir tes enfants naître, grandir, et devenir adultes. Tout ça pour simplement doubler ton argent. Quand tu présentes les choses comme ça, le Livret A apparaît soudain beaucoup moins attractif, n’est-ce pas ?
Maintenant, prenons une assurance-vie en fonds euros qui rapporte 3 % par an (ce qui est plutôt bien pour un fonds euros en 2026). 72 divisé par 3 égale 24 ans. C’est mieux que le Livret A, mais ça reste presque un quart de siècle pour doubler. Passons à un PEA investi en actions avec un rendement historique moyen de 8 % par an sur le long terme. 72 divisé par 8 égale 9 ans. Neuf ans pour doubler ton capital, contre 30 ans pour le Livret A. La différence est vertigineuse. Et si tu trouves un placement à 12 % de rendement annuel ? 72 divisé par 12 égale 6 ans seulement pour doubler.
Tu commences à percevoir la puissance de cette règle ? Elle transforme des pourcentages abstraits en durées concrètes, en années de ta vie. Et quand tu raisonnes en années plutôt qu’en pourcentages, tes décisions financières deviennent soudain beaucoup plus claires. Un placement à 2 % et un placement à 8 %, ce n’est pas « juste 6 points d’écart ». C’est la différence entre doubler ton argent en 36 ans ou en 9 ans. C’est la différence entre un doublement ou quatre doublements sur la même période. Et quatre doublements, ça signifie que 10 000 euros deviennent 160 000 euros au lieu de 20 000 euros. Le même capital de départ, la même durée, mais un résultat huit fois supérieur.
Pourquoi 72 et pas un autre chiffre ?
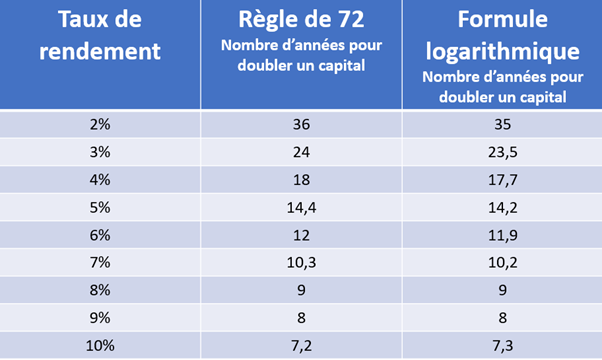
Tu te demandes peut-être pourquoi on utilise 72 et pas un chiffre rond comme 70 ou 100. La réponse vient des mathématiques financières, et plus précisément du logarithme népérien de 2. Quand tu calcules exactement le temps nécessaire pour doubler un capital à un taux d’intérêt composé, tu obtiens la formule suivante : t = ln(2) / ln(1 + r), où t est le temps et r le taux. Pour des taux « normaux » (entre 2 % et 15 %), cette formule donne des résultats très proches de 69,3 divisé par le taux. Mais 69,3 n’est pas un chiffre pratique à diviser de tête.
C’est là que le génie de la règle des 72 intervient. Le nombre 72 est légèrement supérieur à 69,3, ce qui introduit une petite erreur, mais cette erreur est compensée par le fait que les intérêts composés « travaillent » de façon continue plutôt que ponctuelle. Et surtout, 72 est un nombre merveilleusement divisible. Il est divisible par 2, 3, 4, 6, 8, 9, 12, 18, 24 et 36. Cela signifie que pour la plupart des taux de rendement courants, tu peux faire la division de tête instantanément. 72 divisé par 6 ? C’est 12. 72 divisé par 8 ? C’est 9. 72 divisé par 9 ? C’est 8. 72 divisé par 4 ? C’est 18. Aucun calcul compliqué, juste des divisions élémentaires que tu connais depuis l’école primaire.
Il existe des variantes de cette règle. Certains financiers utilisent la règle des 70, qui est légèrement plus précise pour les taux faibles (inférieurs à 5 %). D’autres utilisent la règle des 69, qui est mathématiquement la plus exacte mais beaucoup moins pratique à calculer de tête. En pratique, la règle des 72 offre le meilleur compromis entre précision et facilité de calcul. L’erreur est généralement inférieure à 1 % pour les taux compris entre 4 % et 12 %, ce qui est largement suffisant pour prendre des décisions éclairées.
Une formule vieille de 530 ans
Ce qui est fascinant avec la règle des 72, c’est qu’elle n’a rien de nouveau. Elle a été documentée pour la première fois en 1494 — il y a plus de cinq siècles — par un moine franciscain italien nommé Luca Pacioli. Ce personnage méconnu du grand public était pourtant l’un des esprits les plus brillants de la Renaissance. Ami proche de Léonard de Vinci (qui a d’ailleurs illustré l’un de ses livres), Pacioli est considéré comme le père de la comptabilité moderne. C’est lui qui a formalisé le principe de la partie double que tous les comptables utilisent encore aujourd’hui.
Dans son ouvrage « Summa de arithmetica, geometria, proportioni et proportionalità », Pacioli présente la règle des 72 comme un outil pratique pour les marchands et les banquiers de l’époque. Il écrit, en substance, que pour connaître le nombre d’années nécessaires pour qu’un capital double à un taux donné d’intérêt composé, il suffit de diviser 72 par ce taux. Cinq cent trente ans plus tard, la formule n’a pas pris une ride. Elle est toujours aussi précise, toujours aussi pratique, toujours aussi puissante. Et pourtant, l’immense majorité des gens ne la connaissent pas.
Cette ignorance généralisée n’est pas un hasard. La règle des 72 est trop simple, trop efficace, trop démystifiante pour être enseignée au grand public. Elle permet de comparer des placements en deux secondes, de démasquer les promesses irréalistes, de comprendre intuitivement ce que signifie vraiment un taux de rendement. En un mot, elle rend les épargnants autonomes. Et des épargnants autonomes, c’est moins pratique pour ceux qui vivent de commissions sur des produits financiers complexes. Je ne dis pas qu’il y a une conspiration pour cacher cette formule. Je dis simplement qu’il n’y a aucun intérêt commercial à la populariser.
🔍 Les 7 applications qui changent tout
Application 1 : Comparer des placements en 10 secondes
La première application de la règle des 72, et la plus évidente, c’est la comparaison instantanée de placements. Quand ton banquier te présente un produit avec un rendement de 3 %, tu peux immédiatement visualiser ce que cela signifie : 72/3 = 24 ans pour doubler. Quand ton assureur te vante un contrat à 4 %, tu sais que c’est 72/4 = 18 ans pour doubler. Et quand un conseiller en gestion de patrimoine te propose un investissement à 7 %, tu calcules instantanément : 72/7 ≈ 10 ans pour doubler.
Faisons le tour des principaux placements disponibles en France avec cette grille de lecture. Le Livret A à 2,4 % : 30 ans pour doubler. Le LEP (Livret d’Épargne Populaire) à 3,5 % : environ 20 ans pour doubler. Le fonds euros moyen d’une assurance-vie à 3 % : 24 ans pour doubler. Les SCPI avec un rendement moyen de 4,5 % : 16 ans pour doubler. Un PEA en ETF World avec un rendement historique de 8 % : 9 ans pour doubler. L’immobilier locatif avec un rendement net de 5 % : 14 ans pour doubler. Et les cryptomonnaies ? Si Bitcoin continue sa progression historique d’environ 50 % par an en moyenne, c’est 72/50 = 1,4 an pour doubler. Mais attention, cette moyenne masque une volatilité extrême et des années de baisse brutale.
Ce tableau mental te permet de prendre du recul face aux discours commerciaux. Quand quelqu’un te dit « ce placement rapporte 3 % garanti », tu traduis immédiatement : « il me faut 24 ans pour doubler mon argent ». Quand on te promet « un rendement supérieur à 10 % », tu calcules : moins de 7 ans pour doubler, ce qui implique un risque significatif. La règle des 72 transforme des pourcentages abstraits en durées concrètes, et les durées sont beaucoup plus parlantes pour notre cerveau humain.
Application 2 : Comprendre ce que l’inflation te vole
La deuxième application de la règle des 72 est peut-être la plus importante, et paradoxalement la moins connue. Cette règle ne fonctionne pas seulement pour les gains, elle fonctionne aussi pour les pertes. Et la plus grande perte silencieuse que tu subis chaque année, c’est l’inflation. L’inflation, c’est la hausse générale des prix qui érode ton pouvoir d’achat année après année. Et avec la règle des 72, tu peux calculer exactement à quelle vitesse cette érosion se produit.
Prenons une inflation moyenne de 3 % par an, ce qui correspond à peu près à ce que nous avons connu ces dernières années en France. Applique la règle des 72 : 72/3 = 24 ans pour que ton pouvoir d’achat soit divisé par deux. Autrement dit, si tu gardes 100 000 euros sous ton matelas sans les investir, dans 24 ans ces 100 000 euros n’auront plus que le pouvoir d’achat de 50 000 euros actuels. Tu n’auras rien perdu nominalement — tu auras toujours 100 000 euros — mais tu pourras acheter deux fois moins de choses avec. C’est une perte invisible, silencieuse, mais absolument réelle.
Et si l’inflation monte à 5 % comme nous l’avons vu en 2022-2023 ? 72/5 = 14 ans pour perdre la moitié de ton pouvoir d’achat. Quatorze ans seulement. C’est le temps qui sépare la naissance de ton enfant de son entrée au lycée. Pendant ce temps, l’argent que tu aurais mis de côté pour ses études aurait perdu la moitié de sa valeur réelle. Cette réalité mathématique devrait convaincre n’importe qui que « ne rien faire » avec son argent est déjà une décision — et une mauvaise décision. L’inflation est un impôt invisible qui frappe tous ceux qui gardent leur argent en liquide ou sur des comptes non rémunérés.
Maintenant, combinons ces deux applications. Si tu places ton argent sur un Livret A à 2,4 % alors que l’inflation est à 3 %, ton rendement réel est de 2,4 - 3 = -0,6 % par an. Tu perds du pouvoir d’achat même en « épargnant ». Pour que ton épargne conserve simplement sa valeur, il faut que le rendement soit au moins égal à l’inflation. Et pour que ton épargne progresse réellement, il faut que le rendement soit supérieur à l’inflation. C’est ce qu’on appelle le rendement réel, et c’est le seul qui compte vraiment.
Application 3 : Le vrai coût des frais de gestion
Voici une application de la règle des 72 que les banquiers détestent : elle révèle le coût réel des frais de gestion sur le long terme. Ces frais semblent toujours dérisoires quand on les présente en pourcentage annuel. « 2 % de frais de gestion, ce n’est pas grand-chose », te dit le conseiller. Ah bon ? Appliquons la règle des 72 pour voir ce que ça donne réellement.
Si tes frais de gestion sont de 2 % par an, la règle des 72 nous dit que 72/2 = 36 ans pour que ces frais consomment la moitié de ton capital initial. Autrement dit, sur 36 ans, tu auras donné en frais l’équivalent de la moitié de ce que tu as investi au départ. Et ce n’est pas tout : ces frais s’appliquent sur un capital qui aurait dû croître, donc le manque à gagner est encore plus important. En réalité, des frais de 2 % par an sur 30 ans peuvent te coûter jusqu’à 40 % de la valeur finale de ton portefeuille par rapport à un placement sans frais.
Comparons deux investisseurs qui placent chacun 100 000 euros pendant 30 ans à un rendement brut de 8 % par an. Le premier investit dans un ETF à frais réduits (0,2 % par an), le second dans un fonds actif classique (2 % par an). Après 30 ans, le premier aura environ 925 000 euros (rendement net de 7,8 %). Le second aura environ 570 000 euros (rendement net de 6 %). La différence ? 355 000 euros partis en frais ! Trois cent cinquante-cinq mille euros de différence pour le même capital de départ et le même rendement brut. C’est le prix de 1,8 point de frais supplémentaires par an sur 30 ans.
Cette application de la règle des 72 devrait te rendre allergique aux frais excessifs. Chaque fois qu’on te propose un placement, demande les frais totaux (frais de gestion, frais d’entrée, frais d’arbitrage, frais de sortie) et fais le calcul. Un fonds qui prélève 2,5 % de frais par an aura consommé la moitié de ton capital initial en 72/2,5 = 29 ans. Un ETF à 0,2 % mettra 72/0,2 = 360 ans à faire la même chose. La différence est colossale, et elle explique pourquoi la gestion passive (ETF) surperforme la gestion active (fonds classiques) dans la grande majorité des cas sur le long terme.
Application 4 : Ton crédit immobilier à l’envers
La règle des 72 fonctionne aussi dans l’autre sens : elle permet de comprendre à quelle vitesse une dette grandit si tu ne la rembourses pas. C’est particulièrement utile pour évaluer le danger réel des crédits à la consommation et des crédits revolving. Ces crédits affichent des taux d’intérêt qui semblent « raisonnables » quand on les voit en pourcentage, mais qui deviennent effrayants quand on les traduit en temps de doublement.
Prenons un crédit revolving typique à 18 % de taux d’intérêt annuel (ce qui est malheureusement courant pour ce type de crédit). Appliquons la règle des 72 : 72/18 = 4 ans pour que ta dette double si tu ne rembourses que les intérêts. Tu empruntes 5 000 euros, et si tu ne rembourses que le minimum (qui couvre à peine les intérêts), tu devras 10 000 euros dans 4 ans, 20 000 euros dans 8 ans, 40 000 euros dans 12 ans. C’est une spirale infernale qui explique pourquoi tant de ménages se retrouvent surendettés avec des crédits revolving.
Même un crédit à la consommation « classique » à 8 % double en 72/8 = 9 ans si tu ne le rembourses pas. Et un découvert bancaire à 15 % (taux courant pour les découverts non autorisés) double en 72/15 = 4,8 ans. Ces chiffres devraient te convaincre d’une règle simple : ne jamais emprunter à un taux supérieur au rendement de tes placements. Si tu paies 8 % d’intérêts sur un crédit conso alors que ton épargne rapporte 3 %, tu perds de l’argent à chaque instant. Il vaut mieux puiser dans ton épargne pour rembourser le crédit, même si psychologiquement c’est difficile.
À l’inverse, la règle des 72 peut te rassurer sur un crédit immobilier bien négocié. Avec un taux de 3,5 % actuellement, ta dette ne doublerait qu’en 72/3,5 = 20 ans si tu ne remboursais rien. Mais comme tu rembourses du capital chaque mois, ta dette diminue progressivement. Et si l’immobilier se valorise de 2-3 % par an en moyenne sur le long terme, ton patrimoine net progresse. Un crédit immobilier à taux raisonnable pour acheter un bien de qualité est un « bon » endettement. Un crédit revolving pour financer des achats de consommation est un « mauvais » endettement. La règle des 72 permet de quantifier précisément cette différence.
Application 5 : L’immobilier locatif décrypté
L’investissement locatif est souvent présenté avec des rendements bruts alléchants : « 7 % de rendement brut ! », « 8 % dans cette ville ! ». Mais entre le rendement brut affiché et le rendement net réellement perçu, il y a un monde. La règle des 72 permet de mesurer concrètement l’impact de cet écart sur le temps nécessaire pour rentabiliser ton investissement.
Prenons un appartement acheté 200 000 euros qui génère 14 000 euros de loyers annuels. Le rendement brut est de 14 000 / 200 000 = 7 %. Avec la règle des 72, ton capital doublerait en 72/7 ≈ 10 ans grâce aux loyers. Mais attends : il faut retirer les charges de copropriété non récupérables (disons 1 000 €), la taxe foncière (1 500 €), l’assurance PNO (200 €), les frais de gestion si tu délègues (700 €), la provision pour travaux (500 €), et les impôts sur les revenus fonciers (variable selon ta TMI, mais facilement 2 000 € pour quelqu’un à 30 %). Au final, il te reste peut-être 8 000 euros nets, soit un rendement net de 4 %. Et là, le temps de doublement passe à 72/4 = 18 ans.
La différence entre 10 ans et 18 ans pour doubler, c’est énorme. C’est presque le double du temps. Et encore, je n’ai pas compté les périodes de vacance locative, les impayés éventuels, les travaux imprévus. Le rendement réel d’un investissement locatif est souvent inférieur de 2 à 3 points au rendement brut affiché. Quand un agent immobilier te vante un « 7 % de rentabilité », traduis immédiatement : « 4 à 5 % net si tout se passe bien, soit 14 à 18 ans pour doubler mon capital ». C’est toujours intéressant, mais c’est beaucoup moins spectaculaire que le chiffre d’accroche.
Cette application de la règle des 72 te permet aussi de comparer l’immobilier locatif avec d’autres placements sur une base équitable. Un PEA investi en ETF World à 8 % net (après impôts grâce à l’enveloppe fiscale avantageuse) double en 9 ans. Un appartement locatif à 4 % net double en 18 ans. Pour que l’immobilier soit plus intéressant que le PEA, il faut compter sur la plus-value à la revente et sur l’effet de levier du crédit. Ce sont deux avantages réels de l’immobilier, mais ils ne sont pas garantis et comportent leurs propres risques.
Application 6 : Planifier ta retraite sur un coin de table
Voici l’une des applications les plus puissantes de la règle des 72 : la planification de retraite simplifiée. Avec cette formule, tu peux estimer en quelques minutes combien tu dois investir pour atteindre un objectif de capital à un horizon donné. Pas besoin de tableur Excel, pas besoin de simulateur en ligne, juste une série de divisions simples.
La méthode repose sur le concept de « nombre de doublements ». Supposons que tu aies 30 ans et que tu veuilles avoir 500 000 euros de capital à 60 ans pour ta retraite. Tu as donc 30 ans devant toi. Si tu investis avec un rendement moyen de 8 % par an, ton capital double tous les 72/8 = 9 ans. En 30 ans, tu auras donc environ 30/9 ≈ 3,3 doublements. Trois doublements, ça signifie que ton capital est multiplié par 2×2×2 = 8. Le petit bout de doublement supplémentaire (0,3) ajoute environ 25 %. Au total, ton capital sera multiplié par environ 10.
Pour avoir 500 000 euros dans 30 ans avec ce rendement, il te faut donc un capital de départ de 500 000 / 10 = 50 000 euros. Si tu n’as pas 50 000 euros à investir d’un coup, tu peux étaler. En investissant régulièrement, la formule est un peu différente mais le principe reste le même. Avec des versements réguliers de 500 euros par mois pendant 30 ans à 8 %, tu atteindras environ 750 000 euros grâce à l’effet des intérêts composés. Le capital investi (500 × 12 × 30 = 180 000 euros) aura généré 570 000 euros de gains, soit plus de trois fois la mise de départ.
Maintenant, comparons deux scénarios avec la règle des 72 pour comprendre l’importance de commencer tôt. Scénario 1 : Tu commences à 25 ans, tu investis 200 euros par mois pendant 40 ans à 8 %. Tu auras environ 700 000 euros à 65 ans. Scénario 2 : Tu commences à 35 ans, tu investis 400 euros par mois (le double !) pendant 30 ans à 8 %. Tu auras environ 600 000 euros à 65 ans. Celui qui investit moitié moins mais commence 10 ans plus tôt finit avec plus d’argent ! C’est la magie des intérêts composés, et la règle des 72 permet de comprendre intuitivement pourquoi.
Application 7 : Négocier ton salaire avec la règle des 72
Dernière application, et peut-être la plus surprenante : la règle des 72 peut t’aider à négocier ton salaire et à mesurer l’impact réel des augmentations sur ta carrière. Parce qu’un salaire qui augmente régulièrement bénéficie lui aussi de l’effet composé, et cet effet est considérable sur une carrière de 40 ans.
Imaginons que tu gagnes 40 000 euros bruts annuels en début de carrière. Si tu obtiens des augmentations moyennes de 2 % par an (ce qui correspond à peu près à l’inflation), ton salaire doublera en 72/2 = 36 ans. À la fin de ta carrière (40 ans plus tard), tu gagneras environ 88 000 euros bruts. Pas mal, mais tu auras simplement maintenu ton pouvoir d’achat. Maintenant, si tu obtiens des augmentations moyennes de 5 % par an (en changeant de poste, en négociant, en développant tes compétences), ton salaire double en 72/5 = 14 ans. Après 40 ans de carrière, tu gagneras environ 280 000 euros bruts — plus de trois fois plus que dans le premier scénario.
Cette différence de 3 points d’augmentation annuelle (5 % vs 2 %) se traduit par un écart colossal sur une carrière complète. En cumulant tous les salaires perçus sur 40 ans, le scénario à 5 % génère deux fois plus de revenus totaux que le scénario à 2 %. Et cela ne compte pas les avantages connexes : cotisations retraite plus élevées, capacité d’emprunt supérieure, épargne plus importante. Une augmentation de salaire n’est pas un événement ponctuel, c’est un changement de trajectoire qui se compose année après année.
La règle des 72 te donne aussi un argument chiffré pour négocier. Quand tu demandes 5 % d’augmentation au lieu des 2 % qu’on te propose, tu peux expliquer : « Avec 2 %, mon salaire double en 36 ans. Avec 5 %, il double en 14 ans. Sur le reste de ma carrière, cette différence représente des centaines de milliers d’euros. » Ce discours, appuyé sur des chiffres concrets, est beaucoup plus convaincant qu’une simple demande émotionnelle. La règle des 72 transforme une négociation de salaire en discussion rationnelle sur la valeur à long terme.
Mais l’application va encore plus loin. Prenons le cas d’un changement d’emploi. Tu hésites entre rester dans ton entreprise actuelle avec une augmentation de 3 % et partir chez un concurrent qui te propose 15 % de plus immédiatement. Beaucoup de gens se focalisent sur le gain immédiat (« 15 % de plus, c’est super ! ») sans mesurer l’impact à long terme. Faisons le calcul. Si tu restes et que tu obtiens 3 % par an, ton salaire double en 24 ans. Si tu pars et que tu obtiens ensuite les mêmes 3 % par an, ton salaire de départ est 15 % plus élevé, et il double aussi en 24 ans — mais depuis une base plus haute. Sur 20 ans de carrière restante, le fait d’avoir changé d’emploi avec 15 % d’augmentation te rapportera l’équivalent de 3 années de salaire supplémentaires en cumulé. Trois années de salaire. Ça vaut le coup de sortir de sa zone de confort, non ?
Et si on combine les deux ? Si le nouvel emploi te permet aussi d’avoir des augmentations de 5 % par an au lieu de 3 %, l’effet est exponentiel. La base plus haute (+ 15 %) combinée à une croissance plus rapide (5 % vs 3 %) aboutit à un salaire final qui peut être le double de ce que tu aurais eu en restant. La règle des 72 révèle que les décisions de carrière qui semblent marginales (« juste quelques pourcents de différence ») ont en réalité des conséquences massives sur le patrimoine d’une vie.
📈 L’intérêt composé - la 8ème merveille du monde
Tu as certainement déjà entendu cette phrase attribuée à Albert Einstein : « L’intérêt composé est la huitième merveille du monde. Celui qui le comprend le gagne, celui qui ne le comprend pas le paie. » C’est une citation magnifique, souvent utilisée dans les livres de finance personnelle et les séminaires d’investissement. Il y a juste un petit problème : Einstein ne l’a probablement jamais prononcée. Les historiens n’ont trouvé aucune trace de cette citation dans les écrits ou les discours authentifiés du célèbre physicien. Elle est apparue dans les années 1980, bien après sa mort, et lui a été attribuée pour donner du poids au message.
Mais peu importe qui l’a vraiment dite, la citation est parfaitement exacte sur le fond. L’intérêt composé — le fait de gagner des intérêts sur ses intérêts — est probablement le concept financier le plus puissant qui existe. C’est lui qui permet à de petites sommes investies tôt de devenir des fortunes. C’est lui qui explique pourquoi Warren Buffett, qui a commencé à investir à 11 ans, est devenu l’un des hommes les plus riches du monde. C’est lui aussi qui piège les personnes endettées dans des spirales infernales quand il joue contre elles. Et la règle des 72 n’est rien d’autre qu’un raccourci pratique pour visualiser les effets de l’intérêt composé.
D’ailleurs, parlons de Warren Buffett puisque son cas illustre parfaitement la puissance de l’intérêt composé. L’« Oracle d’Omaha » a aujourd’hui une fortune estimée à plus de 130 milliards de dollars. Ce qui est stupéfiant, c’est que 99 % de cette fortune a été accumulée après ses 50 ans. À 50 ans, Buffett « ne pesait que » 376 millions de dollars. Impressionnant, mais loin des 130 milliards actuels. C’est entre 50 et 93 ans que sa fortune a explosé, passant de 376 millions à 130 milliards — soit une multiplication par 345. Pourquoi ? Parce que l’intérêt composé a besoin de temps pour déployer toute sa puissance. Les premières décennies construisent la base, les dernières décennies récoltent les fruits. Buffett n’est pas devenu riche parce qu’il est le meilleur investisseur du monde (même si c’est un excellent investisseur). Il est devenu riche parce qu’il est un bon investisseur depuis 80 ans.
La magie des intérêts sur les intérêts
Pour comprendre vraiment la puissance de l’intérêt composé, prenons un exemple détaillé. Tu investis 10 000 euros à un taux de 7 % par an pendant 40 ans. Voici ce qui se passe année après année. La première année, tu gagnes 7 % de 10 000 euros, soit 700 euros. Ton capital passe à 10 700 euros. La deuxième année, tu gagnes 7 % de 10 700 euros, soit 749 euros. Ton capital passe à 11 449 euros. La troisième année, tu gagnes 7 % de 11 449 euros, soit 801 euros. Et ainsi de suite, avec des gains qui augmentent chaque année parce qu’ils sont calculés sur un capital de plus en plus gros.
Au bout de 10 ans, ton capital aura doublé une première fois pour atteindre environ 19 700 euros. Les gains annuels seront d’environ 1 380 euros, soit presque le double des 700 euros initiaux. Au bout de 20 ans, après un deuxième doublement, ton capital atteindra environ 38 700 euros. Les gains annuels seront d’environ 2 700 euros. Au bout de 30 ans, troisième doublement, ton capital sera d’environ 76 100 euros. Les gains annuels dépasseront les 5 300 euros — presque autant que ta mise de départ, générés en une seule année ! Et au bout de 40 ans, ton capital atteindra environ 150 000 euros. Les gains de la dernière année seront de plus de 10 000 euros, soit l’équivalent de ton investissement initial, générés en seulement 12 mois.
Cette progression fulgurante s’explique par la nature exponentielle de l’intérêt composé. Au début, les gains semblent modestes : 700 euros, 750 euros, 800 euros… Mais à la fin, ils explosent : 8 000 euros, 9 000 euros, 10 000 euros par an. C’est ce qu’on appelle parfois le « graphique en crosse de hockey » : une progression lente au début qui s’accélère brutalement à la fin. Et c’est pourquoi le temps est la variable la plus importante dans l’équation de l’enrichissement. Avec suffisamment de temps, même de petits montants investis régulièrement deviennent des sommes considérables.
Pourquoi le temps bat le montant
Cette réalité mathématique a une conséquence contre-intuitive : commencer tôt est plus important qu’investir gros. Pour illustrer ce point, comparons deux investisseurs fictifs que nous appellerons Marie et Thomas. Marie commence à investir 200 euros par mois à 25 ans et continue jusqu’à 35 ans, puis elle arrête complètement. Elle aura investi pendant 10 ans, soit un total de 24 000 euros. Thomas, lui, ne commence qu’à 35 ans mais investit 400 euros par mois (le double de Marie) jusqu’à 65 ans, soit pendant 30 ans. Il aura investi 144 000 euros au total, six fois plus que Marie.
Avec un rendement de 8 % par an, qui aura le plus d’argent à 65 ans ? Contre toute attente, c’est Marie ! Son capital aura atteint environ 780 000 euros, tandis que celui de Thomas plafonnerait à environ 590 000 euros. Marie, qui a investi six fois moins d’argent mais a commencé dix ans plus tôt, finit avec 190 000 euros de plus. Comment est-ce possible ? Parce que ses 24 000 euros ont eu 40 ans pour composer (de 25 à 65 ans), tandis que les premiers 400 euros de Thomas n’ont eu que 30 ans pour composer (de 35 à 65 ans). Les dix années supplémentaires de composition ont généré plus de richesse que les 120 000 euros d’investissement supplémentaire de Thomas.
Cette démonstration devrait convaincre n’importe qui de l’importance de commencer à investir le plus tôt possible, même avec de petites sommes. Un jeune de 20 ans qui investit 100 euros par mois finira plus riche qu’un quadragénaire qui investit 300 euros par mois, toutes choses égales par ailleurs. Le temps est le multiplicateur le plus puissant de l’intérêt composé, et c’est une ressource qui ne se rattrape jamais. Chaque année qui passe sans investir est une année de composition perdue à jamais.
Les trois ennemis de l’intérêt composé
L’intérêt composé est une force puissante, mais elle peut être neutralisée par trois ennemis redoutables qu’il faut apprendre à combattre : les frais, l’inflation et les impôts.
Les frais sont l’ennemi le plus sournois parce qu’ils composent contre toi. Nous l’avons vu plus haut : 2 % de frais annuels finissent par consumer la moitié de ton capital initial sur le long terme. Et ces frais ne se contentent pas de prélever une part de tes gains — ils réduisent aussi la base sur laquelle les gains futurs seront calculés. Chaque euro parti en frais est un euro qui ne composera plus jamais. C’est pourquoi la chasse aux frais devrait être une obsession pour tout investisseur de long terme. Prenons un exemple parlant : si tu investis 100 000 euros à 7 % brut pendant 30 ans, avec des frais de 0,3 % (ETF) tu obtiens 700 000 euros, avec des frais de 2 % (fonds classique) tu obtiens 475 000 euros. Les frais t’ont coûté 225 000 euros. C’est plus du double de ton investissement initial, parti en fumée dans les poches des intermédiaires.
L’inflation est l’ennemi le plus pernicieux parce qu’elle est invisible. Tes relevés de compte affichent des chiffres en hausse, mais ton pouvoir d’achat peut stagner ou même diminuer. Si ton placement rapporte 4 % mais que l’inflation est de 3 %, ton rendement réel n’est que de 1 %. Et avec 1 % de rendement réel, ton pouvoir d’achat ne double qu’en 72/1 = 72 ans ! Pour combattre l’inflation, il faut investir dans des actifs dont le rendement dépasse structurellement la hausse des prix : actions, immobilier, matières premières. Historiquement, les actions ont rapporté environ 7 % par an en termes réels (après inflation) sur le très long terme, tandis que les obligations n’ont rapporté que 2-3 % réels et le cash a simplement maintenu son pouvoir d’achat (0 % réel). C’est pourquoi les personnes qui gardent toute leur épargne sur des livrets « pour ne pas prendre de risques » prennent en réalité le risque de voir leur patrimoine fondre lentement mais sûrement.
Les impôts sont l’ennemi le plus prévisible, et donc le plus facile à combattre avec une bonne stratégie. En France, les gains financiers sont taxés à 30 % (flat tax) ou au barème progressif de l’IR selon ce qui est plus avantageux. Mais certaines enveloppes fiscales permettent de réduire ou de différer cette imposition : le PEA exonère les plus-values après 5 ans (hors prélèvements sociaux), l’assurance-vie bénéficie d’un abattement après 8 ans, le PER permet de déduire les versements de ton revenu imposable. Utiliser ces enveloppes, c’est laisser l’intérêt composé travailler à plein régime sans que le fisc ne vienne couper l’élan chaque année.
Pour illustrer l’impact des impôts sur la composition, prenons deux investisseurs qui placent 10 000 euros à 8 % pendant 30 ans. Le premier utilise un compte-titres ordinaire et paie la flat tax de 30 % sur ses gains chaque année. Le second utilise un PEA et ne paie que 17,2 % de prélèvements sociaux à la sortie après 30 ans. Le premier aura environ 57 000 euros au bout de 30 ans (rendement effectif de 5,6 % après impôts). Le second aura environ 84 000 euros après impôts à la sortie. La différence ? 27 000 euros en plus pour le second, simplement parce qu’il a laissé l’intérêt composé travailler sans interruption fiscale. C’est le principe du « report d’imposition » : plus tu repousses le moment de payer des impôts, plus ton capital a le temps de grossir. Et plus ton capital est gros au moment de payer, plus tu profites de l’effet composé.
🧪 La règle des 72 dans la vie réelle
Pour que la règle des 72 passe de concept abstrait à outil concret, laisse-moi te raconter trois histoires vraies (les prénoms ont été changés) qui illustrent la puissance — ou le danger — de l’intérêt composé.
L’histoire de Sophie, 28 ans, qui a découvert la règle trop tard. Sophie a commencé à travailler à 23 ans avec un bon salaire (45 000 euros bruts). Pendant cinq ans, elle a dépensé l’essentiel de ses revenus : appartement en centre-ville, voyages, sorties, vêtements de marque. « J’ai le temps d’épargner plus tard », se disait-elle. À 28 ans, elle rencontre un conseiller financier qui lui explique la règle des 72. Elle fait le calcul : si elle avait investi 500 euros par mois à 8 % depuis ses 23 ans, elle aurait aujourd’hui 36 000 euros (30 000 euros investis + 6 000 euros de gains). Ce n’est pas énorme. Mais projetons ce capital sur 37 ans jusqu’à sa retraite à 65 ans. Sans ajouter un centime de plus, ces 36 000 euros deviendraient 580 000 euros grâce aux 4 doublements successifs. Sophie réalise qu’elle a « perdu » non pas 30 000 euros, mais potentiellement plus de 500 000 euros de capital retraite. Elle commence immédiatement à investir 800 euros par mois pour rattraper — mais elle sait qu’elle ne rattrapera jamais complètement ces cinq années perdues.
L’histoire de Marc, 45 ans, piégé par les frais. Marc investit depuis 20 ans dans une assurance-vie gérée par sa banque. Chaque année, il verse 5 000 euros. Il est plutôt content : son capital affiche 180 000 euros, alors qu’il n’a versé que 100 000 euros. Mais un jour, il découvre la règle des 72 et calcule son rendement réel. 180 000 / 100 000 = 1,8, soit 80 % de gain en 20 ans. Cela correspond à un rendement annuel d’environ 3 %. Or, pendant ces 20 ans, la Bourse a rapporté en moyenne 7-8 % par an. Que s’est-il passé ? Les frais. Son assurance-vie prélève 0,9 % de frais de gestion sur le contrat, plus 1,8 % de frais de gestion sur les unités de compte, plus 3 % de frais d’entrée sur chaque versement. Au total, près de 3-4 % de frais annuels qui ont amputé son rendement de moitié. S’il avait investi dans un PEA avec des ETF à 0,3 % de frais, ses 100 000 euros seraient devenus 330 000 euros au lieu de 180 000 euros. Les frais lui ont coûté 150 000 euros sur 20 ans.
L’histoire de Claire et Thomas, le couple qui a tout compris. Claire et Thomas se sont mariés à 25 ans avec un objectif clair : acheter leur résidence principale à 35 ans avec un gros apport, puis être « libres financièrement » à 55 ans. Ils ont appliqué la règle des 72 à l’envers. Pour avoir 500 000 euros à 55 ans avec un rendement de 8 %, combien de doublements entre 25 et 55 ans ? 30/9 = 3,3 doublements, soit une multiplication par environ 10. Il leur faut donc 50 000 euros à 25 ans. Impossible pour eux. Mais 10 ans plus tard à 35 ans, après l’achat de leur maison, ils n’ont besoin que de deux doublements (20 ans / 9 = 2,2). Soit un capital de 50 000 / 2,2 doublements ≈ 110 000 euros à placer à 35 ans. C’est leur plan. Ils épargnent agressivement entre 25 et 35 ans pour constituer l’apport immobilier ET les 110 000 euros de capital « retraite anticipée ». À 35 ans, ils achètent leur maison et placent 110 000 euros en PEA. Vingt ans plus tard, à 55 ans, le PEA affiche 490 000 euros (légèrement sous l’objectif à cause de la volatilité, mais dans la cible). Ils peuvent lever le pied. La règle des 72 a guidé leur stratégie pendant 30 ans.
⚠️ Les limites et les pièges
Quand la règle devient imprécise
La règle des 72 est un outil d’approximation remarquablement précis dans la plupart des situations courantes, mais elle a ses limites. Il est important de les connaître pour ne pas faire de calculs erronés dans certains cas particuliers.
La première limite concerne les taux très élevés. Au-delà de 20 % de rendement annuel, la règle des 72 commence à surestimer le temps de doublement. Par exemple, à 24 % de rendement, la règle des 72 prédit un doublement en 72/24 = 3 ans, alors que le calcul exact donne environ 2,9 ans. L’erreur reste acceptable (3 %). Mais à 50 % de rendement, la règle prédit 72/50 = 1,44 ans, alors que le calcul exact donne 1,71 ans — une erreur de 15 %. Pour des taux supérieurs à 20 %, il vaut mieux utiliser la règle des 69 (plus précise mathématiquement) ou un calcul exact.
La deuxième limite concerne les taux très faibles. En dessous de 2 %, la règle des 72 sous-estime légèrement le temps de doublement. À 1 % de rendement, la règle prédit 72 ans pour doubler, alors que le calcul exact donne 69,7 ans. L’erreur est d’environ 3 %, ce qui reste acceptable. Mais pour des calculs très précis sur des placements à faible rendement (livrets, fonds euros), la règle des 70 est légèrement plus exacte.
En pratique, pour les taux compris entre 4 % et 12 % — ce qui couvre la grande majorité des placements courants — la règle des 72 est d’une précision remarquable, avec des erreurs généralement inférieures à 1 %. C’est dans cette plage qu’elle est le plus utile et le plus fiable.
Les rendements ne sont pas constants
La deuxième grande limite de la règle des 72 est qu’elle suppose un rendement constant année après année. Or, dans la vraie vie, les rendements fluctuent. La Bourse peut faire +20 % une année et -15 % l’année suivante. L’immobilier peut stagner pendant cinq ans puis bondir de 30 %. Ces variations ont un impact sur le temps réel de doublement qui n’est pas capturé par la règle des 72.
Et voici le piège le plus vicieux : la moyenne arithmétique des rendements n’est pas égale à la moyenne géométrique (celle qui compte vraiment pour la composition). Exemple : si ton placement fait +50 % la première année puis -50 % la deuxième année, tu pourrais penser que la moyenne est (50 - 50) / 2 = 0 %, donc que tu es revenu à ton point de départ. Faux ! Si tu as investi 100 euros, après la première année tu as 150 euros. Après la deuxième année (−50 %), tu as 75 euros. Tu as perdu 25 % de ton capital initial alors que la « moyenne » des rendements était de 0 %.
Ce phénomène s’appelle la volatilité drag (ou « érosion par la volatilité »). Plus les rendements sont volatils, plus la moyenne géométrique (le rendement réellement perçu) est inférieure à la moyenne arithmétique (le rendement « affiché »). C’est pourquoi deux placements avec le même rendement moyen affiché peuvent donner des résultats très différents si l’un est beaucoup plus volatil que l’autre. La règle des 72 ne capture pas cette nuance — elle suppose implicitement des rendements stables.
La règle des 72 comme détecteur de bullshit
Malgré ses limites, la règle des 72 a une application défensive extraordinaire : c’est un excellent détecteur d’arnaques et de promesses irréalistes. Quand quelqu’un te promet des rendements mirobolants, sors la règle des 72 et vérifie si ça tient la route.
« Doublez votre capital en 3 ans ! » C’est du 72/3 = 24 % de rendement annuel. C’est possible en Bourse sur une période exceptionnelle, mais personne ne peut le garantir. Si on te le garantit, c’est une arnaque (probablement un schéma de Ponzi). « Rendement garanti de 12 % ! » Doublement en 6 ans, ce qui est extraordinaire pour un placement « garanti ». Les seuls placements vraiment garantis (livrets, fonds euros) rapportent 2 à 4 %. Un « 12 % garanti » est soit un mensonge, soit un placement à très haut risque déguisé.
À l’inverse, si on te propose un placement honnête à 5-6 % de rendement attendu avec les risques clairement expliqués, c’est cohérent avec les rendements historiques de nombreuses classes d’actifs (immobilier locatif, obligations d’entreprises, fonds diversifiés). La règle des 72 te dit : doublement en 12 à 14 ans, ce qui est réaliste. Tu peux étudier l’offre sereinement.
La règle générale est simple : plus le temps de doublement promis est court, plus il faut être méfiant. Doubler en 3 ans (24 % par an) : extrêmement risqué ou frauduleux. Doubler en 6 ans (12 % par an) : très ambitieux, nécessite une vérification approfondie. Doubler en 9-10 ans (7-8 % par an) : réaliste pour des actions diversifiées sur le long terme. Doubler en 15-20 ans (4-5 % par an) : réaliste pour des placements prudents. Doubler en 30+ ans (2-3 % par an) : typique des livrets et fonds euros, peu de risque mais peu de rendement.
🎯 Applications avancées
La règle des 72 pour l’inflation cachée
Au-delà de l’inflation officielle mesurée par l’INSEE, il existe des inflations sectorielles beaucoup plus élevées qui grignotent ton pouvoir d’achat dans des domaines spécifiques. La règle des 72 permet de mesurer leur impact réel.
L’immobilier dans les grandes villes a augmenté en moyenne de 5 à 7 % par an sur les vingt dernières années. Appliquons la règle des 72 : les prix doublent tous les 10 à 14 ans. Si tu n’achètes pas maintenant, tu devras payer le double dans 10-14 ans. Ou, vu autrement, si tu économises pour un apport sans investir cet argent, ton pouvoir d’achat immobilier se divise par deux en 10-14 ans même si ton compte en banque grossit. C’est la course impossible de l’épargnant qui met de côté pour acheter : s’il place son argent à 3 % alors que l’immobilier monte de 6 %, il recule chaque année au lieu d’avancer. La seule solution est d’investir son épargne à un rendement supérieur à l’inflation immobilière — ou d’acheter le plus tôt possible avec un crédit, en utilisant l’effet de levier à ton avantage.
Les frais de scolarité dans l’enseignement supérieur privé augmentent d’environ 4 % par an en France (et beaucoup plus aux États-Unis). À ce rythme, ils doublent en 72/4 = 18 ans. Si tu veux financer les études de ton enfant qui naît aujourd’hui, le coût sera environ le double de ce qu’il est actuellement quand il aura 18 ans. Une école de commerce qui coûte 15 000 euros par an aujourd’hui coûtera 30 000 euros par an dans 18 ans. Sur cinq ans d’études, la facture passera de 75 000 euros à 150 000 euros. Si tu veux anticiper cette dépense, il faut ouvrir un contrat d’assurance-vie ou un PEA dès maintenant et y verser régulièrement. En 18 ans à 7 % de rendement, tu peux transformer 200 euros par mois en plus de 85 000 euros — de quoi couvrir une bonne partie de la facture.
Les dépenses de santé non remboursées augmentent également plus vite que l’inflation générale. Les tarifs des mutuelles progressent de 3 à 5 % par an, soit un doublement tous les 14 à 24 ans. Une mutuelle à 100 euros par mois aujourd’hui pourrait coûter 200 euros dans 15-20 ans. Et avec le vieillissement de la population et le désengagement progressif de la Sécurité sociale, cette tendance risque de s’accélérer.
Ces « inflations cachées » expliquent pourquoi tant de gens ont l’impression de s’appauvrir alors que leur salaire suit l’inflation officielle. Le coût de la vie réel — logement, éducation, santé — augmente plus vite que les statistiques générales. La règle des 72 te permet de quantifier ces écarts et d’adapter ta stratégie d’épargne en conséquence.
Combiner plusieurs doublements
Une technique avancée consiste à chaîner les doublements pour calculer des multiplications plus importantes. On sait que 10 doublements multiplient par 2^10 = 1 024, soit environ 1 000. Cette propriété permet des calculs rapides impressionnants.
Voici le tableau des multiplications par nombre de doublements, à mémoriser. Un doublement multiplie par 2, deux doublements multiplient par 4, trois doublements par 8, quatre doublements par 16, cinq doublements par 32, six doublements par 64, sept doublements par 128. Avec ce tableau en tête, tu peux faire des projections impressionnantes en quelques secondes.
Par exemple : « Combien aurai-je dans 30 ans si j’investis 50 000 euros à 7 % ? » Temps de doublement : 72/7 ≈ 10 ans. En 30 ans, il y aura 3 doublements. Donc le capital sera multiplié par 2^3 = 8. Résultat : 50 000 × 8 = 400 000 euros. Le calcul exact donne 381 000 euros — notre estimation rapide est à 5 % près, ce qui est excellent pour un calcul mental.
Autre exemple : « Quel rendement me faut-il pour transformer 100 000 euros en 1 million en 25 ans ? » Il faut multiplier par 10, ce qui correspond à environ 3,3 doublements (car 2^3,3 ≈ 10). En 25 ans avec 3,3 doublements, chaque doublement prend 25/3,3 ≈ 7,5 ans. Donc il faut un taux de 72/7,5 ≈ 9,6 % par an. C’est ambitieux mais pas irréaliste pour un portefeuille d’actions diversifié sur 25 ans.
Troisième exemple pratique : « Je veux partir avec 2 millions d’euros. J’ai 40 ans, je vise 65 ans, j’ai actuellement 150 000 euros. Possible ou pas ? » En 25 ans, à 8 %, le capital double 25/9 ≈ 2,8 fois, donc est multiplié par environ 6-7. 150 000 × 6,5 = 975 000 euros. Pas suffisant pour atteindre 2 millions. Il faut soit augmenter le capital initial (en épargnant plus), soit viser un rendement plus élevé (plus de risque), soit repousser la date (travailler plus longtemps), soit réduire l’objectif. La règle des 72 révèle instantanément si un objectif est réaliste ou pas.
La règle inverse : du temps vers le taux
La règle des 72 fonctionne aussi à l’envers. Si tu connais le temps de doublement que tu vises, tu peux calculer le taux nécessaire : Taux = 72 / Temps de doublement.
« Je veux doubler mon capital en 5 ans, quel rendement me faut-il ? » Réponse : 72/5 = 14,4 % par an. C’est très ambitieux et implique des risques significatifs. Seuls des investissements à haut risque (startups, crypto, stock-picking agressif) peuvent potentiellement atteindre ce niveau — avec une probabilité importante de perdre de l’argent aussi.
« Je veux que mon épargne de précaution double en 20 ans sans prendre de risque, quel rendement minimum dois-je trouver ? » Réponse : 72/20 = 3,6 % par an. C’est atteignable avec un LEP (si tu y es éligible) ou une bonne assurance-vie en fonds euros.
« Mon PEL rapporte 1 % (pour les PEL ouverts après 2023), en combien de temps double-t-il ? » Réponse : 72/1 = 72 ans. Oui, tu as bien lu. Soixante-douze ans pour doubler ton capital avec un PEL actuel. C’est plus que l’espérance de vie moyenne. Le PEL n’est plus un placement d’épargne, c’est un droit à un prêt immobilier à taux plafonné — c’est sa seule utilité aujourd’hui.
Cette utilisation inverse te permet de fixer des objectifs réalistes. Si tu veux doubler ton capital en moins de 10 ans, tu sais qu’il te faut plus de 7 % de rendement, ce qui implique de prendre des risques (actions, immobilier). Si tu te contentes de doubler en 20 ans, du 3,6 % suffit, accessible avec des placements beaucoup plus sécurisés. La règle des 72 est une boussole qui t’aide à calibrer tes attentes en fonction de ta tolérance au risque et de ton horizon de temps.
✅ Ton plan d’action
Les 5 questions à te poser maintenant
Après cette longue exploration de la règle des 72, voici les questions concrètes que tu devrais te poser pour optimiser ta stratégie financière.
Question 1 : En combien de temps mon épargne actuelle double-t-elle ? Prends le rendement moyen de tes placements et divise 72 par ce chiffre. Si la réponse est supérieure à 15-20 ans, tu subis probablement l’érosion de l’inflation et tu devrais envisager des placements plus dynamiques. Fais l’exercice maintenant : liste tes placements, note leurs rendements, et calcule. Si ton Livret A représente 80 % de ton épargne, tu sais que cette épargne double en 30 ans — beaucoup trop lent pour construire un patrimoine significatif.
Question 2 : Quel est le coût réel des frais que je paie ? Additionne tous les frais de tes placements (gestion, entrée, arbitrage) et divise 72 par ce total. C’est le temps nécessaire pour que les frais « mangent » la moitié de ton capital initial. Si c’est moins de 40 ans, tu paies trop de frais. Demande à ta banque ou ton assureur un relevé détaillé des frais prélevés l’année dernière. Tu risques d’avoir des surprises désagréables.
Question 3 : Combien de doublements puis-je encore espérer avant ma retraite ? Divise le nombre d’années jusqu’à ta retraite par le temps de doublement de tes placements. Si tu as 35 ans, que tu vises 65 ans, et que tes placements doublent tous les 10 ans, tu as 3 doublements devant toi, soit une multiplication par 8. Si tu as 50 ans, tu n’as plus que 1,5 doublement (multiplication par 3). Cette réalité devrait influencer ton allocation d’actifs : plus tu as de doublements devant toi, plus tu peux prendre de risques.
Question 4 : Mon salaire progresse-t-il plus vite que l’inflation ? Si ton salaire augmente de 2 % par an et l’inflation est à 3 %, tu perds du pouvoir d’achat chaque année. Utilise la règle des 72 pour calculer à quelle vitesse : 72/1 = 72 ans pour perdre la moitié de ton pouvoir d’achat, soit environ 1 % par an de perte. C’est le moment de négocier une augmentation ou de changer d’emploi.
Question 5 : Mes dettes « doublent-elles » plus vite que mes placements ? Si tu as un crédit à 8 % et des placements à 4 %, tes dettes « grandissent » deux fois plus vite que ton épargne. Rembourser le crédit en priorité est mathématiquement la meilleure décision. La seule exception : un crédit immobilier à taux bas (< 3 %) pour ta résidence principale, qui est un « bon » endettement grâce à l’effet de levier.
Le tableau récapitulatif à garder sous le coude
Voici les temps de doublement pour les taux les plus courants, à mémoriser ou à garder accessible pour tes prochaines décisions financières. À 1 % de rendement, ton capital double en 72 ans. À 2 %, il double en 36 ans. À 3 %, en 24 ans. À 4 %, en 18 ans. À 5 %, en 14 ans. À 6 %, en 12 ans. À 7 %, en 10 ans. À 8 %, en 9 ans. À 9 %, en 8 ans. À 10 %, en 7 ans. À 12 %, en 6 ans. Et à 15 %, il double en moins de 5 ans.
Ces chiffres devraient devenir des réflexes. Quand tu entends « 3 % », tu penses immédiatement « 24 ans pour doubler ». Quand tu entends « 8 % », tu penses « 9 ans ». Cette traduction instantanée des pourcentages en durées va transformer ta façon d’évaluer n’importe quelle proposition financière. Tu ne seras plus jamais impressionné par un « 3 % garanti » quand tu sauras que ça signifie un quart de siècle pour doubler.
Les 3 erreurs à éviter absolument
Maintenant que tu maîtrises la règle des 72, voici les trois erreurs classiques que font ceux qui ne la connaissent pas — et que tu vas pouvoir éviter.
Erreur n°1 : Sous-estimer l’impact des « petits » pourcentages. La différence entre 5 % et 7 % de rendement semble anodine (« c’est juste 2 points »). Mais traduite en temps de doublement, c’est 14 ans contre 10 ans, soit 40 % de temps en plus pour atteindre le même objectif. Sur 30 ans, cette « petite » différence se traduit par un capital final quasi doublé. Chaque point de pourcentage compte énormément sur le long terme.
Erreur n°2 : Ignorer les frais parce qu’ils « semblent faibles ». 2 % de frais annuels, ça ne paraît rien. Mais sur 30 ans, ces frais vont engloutir près de la moitié de la performance de ton portefeuille. C’est comme si tu travaillais un jour sur deux pour enrichir ton intermédiaire financier plutôt que toi-même. La chasse aux frais devrait être une obsession.
Erreur n°3 : Attendre d’avoir « assez » pour commencer à investir. C’est l’erreur la plus coûteuse. Chaque année d’attente est une année de composition perdue. 100 euros par mois investis à 25 ans valent plus que 200 euros par mois investis à 35 ans sur le long terme. Le « bon moment » pour commencer, c’était hier. Le deuxième meilleur moment, c’est maintenant. Même avec 50 euros par mois, commence. Tu ajusteras plus tard.
Ce que tu dois retenir
La règle des 72 est bien plus qu’une astuce de calcul mental. C’est une grille de lecture qui te permet de comprendre intuitivement le fonctionnement de l’intérêt composé, la huitième merveille du monde selon la citation (apocryphe) d’Einstein. Elle transforme des pourcentages abstraits en années concrètes, et les années sont une mesure que notre cerveau humain appréhende beaucoup mieux.
Avec cette règle, tu peux désormais comparer n’importe quels placements en quelques secondes, mesurer l’impact réel de l’inflation sur ton pouvoir d’achat, évaluer le coût véritable des frais bancaires, comprendre pourquoi les dettes à taux élevé sont si dangereuses, planifier ta retraite avec des ordres de grandeur réalistes, et détecter les promesses de rendement frauduleuses. C’est un outil simple, puissant, et universel qui t’accompagnera toute ta vie.
Le message le plus important de cette newsletter tient en une phrase : le temps est ton meilleur allié si tu le mets de ton côté, et ton pire ennemi si tu l’ignores. Chaque année qui passe sans investir est une année de composition perdue. Chaque année de frais excessifs est une année de composition volée. Chaque année d’inflation non compensée est une année de pouvoir d’achat détruit. La règle des 72 te permet de quantifier précisément ces mécanismes et de prendre des décisions éclairées.
Maintenant que tu connais cette formule magique, utilise-la. Sors-la à chaque fois qu’on te propose un placement. Applique-la à tes investissements actuels. Calcule combien de doublements tu peux encore espérer avant ta retraite. Et surtout, commence à investir le plus tôt possible, même avec de petites sommes. Parce que le temps, contrairement à l’argent, est une ressource qui ne se rattrape jamais.
La prochaine fois que tu seras face à une décision financière, pose-toi cette simple question : « En combien de temps mon argent double-t-il ? » Si c’est plus de 20 ans, tu perds probablement contre l’inflation. Si c’est moins de 6 ans, on te promet des miracles et tu devrais être très méfiant. Entre 8 et 15 ans, tu es dans la zone des rendements réalistes pour des investissements long terme avec un risque raisonnable. Cette simple grille de lecture va filtrer 90 % des mauvaises décisions et des arnaques.
Et n’oublie pas : la règle des 72 fonctionne dans les deux sens. Elle mesure à quelle vitesse ton patrimoine peut croître, mais aussi à quelle vitesse l’inflation le grignote, à quelle vitesse les frais l’amputent, et à quelle vitesse tes dettes s’accumulent si tu ne les rembourses pas. Maîtriser cette règle, c’est comprendre que les mêmes forces qui peuvent t’enrichir peuvent aussi t’appauvrir. Tout dépend du côté où tu te places.
Tu as maintenant un super-pouvoir financier que 95 % des Français ne possèdent pas. Utilise-le pour toi, pour ta famille, pour ton avenir. Et si cette newsletter t’a été utile, partage-la autour de toi. Parce que la règle des 72, c’est comme un vaccin contre l’illéttrisme financier : plus il y a de gens qui la connaissent, mieux la société se porte.
Vous voulez aller plus loin ?
Je peux répondre aux questions que vous vous posez via Wathsapp, je lance ce service sans frais afin que vous ayez accès à du conseil en finances personnelles en toute simplicité. Le lien : https://wa.me/33613018211
Disclaimer : Ceci n’est pas un conseil en investissement, en tant que CIF, je ne peux donner de conseils avant d’avoir pu comprendre qui vous êtes, vos objectifs de vie, vos contraintes et capacités financières. Tout conseil étant personnalisé, et cette newsletter étant généraliste, soyez vigilant sur vos investissements, peu importe la forme qu’ils prendraient.









C’est bon ça !