🎰 La formule secrète des compteurs de cartes de Vegas
#153, Comment une équation née dans les casinos de Vegas a révolutionné la gestion du risque — et pourquoi elle pourrait changer ta façon d'investir
Mes newsletters sont souvent longues, je vous invite à cliquer sur le bandeau pour lire l'intégralité directement sur Internet. De plus, merci de liker ou partager, cela va permettre de développer encore plus Cash Conseils. Petit sondage à la fin... N'oublie pas aussi de liker, ça m'aide à développer ❤️❤️❤️❤️Déjà 152 éditions de cette newsletter envoyée tous les dimanches
Vous aimez son contenu, je vous invite à cliquer sur le ♥️ au-dessus, ça m’aidera énormément.
On vous a transféré la news et vous voulez vous abonner ? 👇👇👇
Tu peux aussi me poser directement une question sur le sujet que tu veux…
🛎️ Ding Ding Ding, l’espace des liens
💶 Sponsoriser la newsletter : Pour vous adresser à ma communauté
🧑💻 Les réseaux : Linkedin, Youtube, Tiktok
🤝 Se retrouver : RDV, Newsletter, Youtube, tous les liens y sont
🤚 Rejoindre la communauté : sur Whatsapp
⚔️ Un coaching personnel : Prendre RDV
📖 Étude de mon patrimoine gratuite (diffusée…): Je veux que tu étudies mon patrimoine
Au sommaire cette semaine
🗞️ Finance Weekly : les cinq faits marquants de la semaine dernière
🔍 Pourquoi tu mises toujours mal (sans le savoir)
📊 L’équation qui tient sur un post-it
🔎 Les milliardaires qui misent avec une calculette
💥 Survivre ou performer : le vrai choix
🛠️ Comment l’utiliser dès demain (sans être matheux)
Temps de lecture : 8 à 10 minutes selon ta vitesse de lecture
📈 Vous, mes abonnés : Nous sommes à 14 161 abonnés. Les abonnements remontent, si vous pouvez partager la newsletter autour de vous, ce serait top.
⚡ Linkedin : Suivez mes publications quotidiennes sur Linkedin. Des actualités fortes, du décryptage de tendances, tout y est. Voici pour me suivre
On me demande un peu de perso à chaque fois, de life style. Je peux vous dire plusieurs choses :
Cette semaine j’étais à Thonon les Bains, pour suivre un chantier, rudement mené, et fini dans les temps
Mon fils devait faire une pré-sélection en M13 pour l’équipe départementale CD17, mais décalée au vu de la météo… Dommage mais ce n’est que partie remise.
🔥 Plan P continue sur sa lancée
Nouvelle confirmation de taille : Charles de Courson rejoint l’aventure Plan P. Le député, figure incontournable des débats budgétaires à l’Assemblée nationale, viendra partager son expertise sur les finances publiques et leur impact sur ton portefeuille. Après Lionel Causse et la Banque de France, le casting institutionnel prend une autre dimension.
Côté coulisses, l’équipe s’agrandit. On recherche un(e) stagiaire pour nous accompagner dans cette aventure : community management, relations médias, coordination événementielle. Si tu connais quelqu’un de motivé par l’éducation financière et prêt à vivre une expérience intense, fais tourner !
Du 13 au 18 avril 2026, on démocratise les finances personnelles à grande échelle. Plus de 1000 inscrits nous font déjà confiance.
👉 Pas encore inscrit ? C’est gratuit :
👉 Intéressé(e) par le stage ? Écris moi
Bien que je sois le fondateur d’un cabinet en gestion de patrimoine, il est important de souligner que Cash Conseils 💸 opère indépendamment de cette entité. Cette newsletter s'inscrit dans une démarche entièrement dédiée à la pédagogie financière, visant à éduquer et à inspirer un large public sur les fondamentaux de la gestion financière personnelle. Cash Conseils 💸 est conçu pour être une ressource éducative ouverte à tous, sans liens directs avec les services ou les orientations spécifiques du cabinet. L'objectif est de fournir une plateforme neutre et informative, où chacun peut apprendre à naviguer dans l'univers des finances personnelles, en toute indépendance et sans conflit d'intérêts.
🏦🇺🇸 Kevin Warsh nommé à la tête de la Fed : un "changement de régime" en vue Trump nomme Kevin Warsh, critique de longue date de la Fed, pour succéder à Jay Powell — sa confirmation par le Sénat reste à venir. Le futur président veut réduire drastiquement le bilan de la Fed (6 600 Mds$) et recentrer la banque centrale sur son mandat originel, jugeant qu'elle a trop empiété sur le terrain budgétaire. Ses détracteurs au sein de la Fed craignent des coupes dans les effectifs et une refonte brutale des méthodes de travail, tandis que ses partisans y voient une réforme salutaire pour éviter une intervention politique externe.
🇫🇷💻 La France pousse ses fonctionnaires à abandonner Zoom pour “Visio”, une alternative souveraine Le Premier ministre Lecornu ordonne aux ministères d’adopter d’ici fin 2025 “Visio”, un outil de visioconférence développé en interne, au nom de la souveraineté numérique. L’Europe dépend encore à plus de 80% des États-Unis pour ses services numériques — les tensions géopolitiques avec l’administration Trump relancent les efforts de “découplage technologique”. Le scepticisme persiste : les précédentes initiatives françaises (Quaero, cloud souverain) ont échoué faute de qualité suffisante face aux géants américains.
🇸🇦🇦🇪 Tensions Arabie Saoudite-Émirats : les entreprises prises en étau sur les visas Le conflit diplomatique né de la crise yéménite se répercute sur les affaires : des employés de banques, cabinets de conseil et sociétés pétrolières basés aux EAU se voient refuser des visas saoudiens. Avec plus de 20 Mds$ d’échanges bilatéraux, de nombreuses entreprises utilisent Dubaï comme hub régional — certaines contournent le problème via le Qatar ou Bahreïn. Riyad intensifie parallèlement sa pression pour que les multinationales transfèrent leur siège régional dans le royaume, condition sine qua non pour accéder aux marchés publics.
📉🎲 Hedge funds : une corrélation record avec les actions qui inquiète En 2025, les fonds spéculatifs actions ont affiché une corrélation de 0,98 avec le MSCI World — le niveau le plus élevé depuis au moins 5 ans selon BNP Paribas. Si cette exposition a boosté leurs performances (+12,5%, meilleure année depuis 2009), elle interroge sur leur capacité à protéger les investisseurs en cas de krach. Les analystes rappellent que lors des corrections de 2011 et 2022, cette forte corrélation avait amplifié les pertes — un risque à surveiller pour les portefeuilles institutionnels.
🥇💥 Or et argent en chute libre : fin brutale du rally historique L’or dégringole de 11% en une séance (de 5 600$ à 4 800$/oz), l’argent s’effondre de 26% — la pire journée jamais enregistrée pour le métal gris. La nomination de Kevin Warsh à la Fed, jugé plus rigoureux sur l’inflation, a dopé le dollar et déclenché des prises de bénéfices massives sur les valeurs refuges. Après un mois de volatilité record alimenté par les tensions géopolitiques mondiales, les analystes alertent sur un marché “excessivement suracheté” et appellent à la prudence.
Imagine que tu te retrouves face à une opportunité d’investissement exceptionnelle. Les fondamentaux sont solides, les perspectives de croissance sont claires, et tu as fait toutes tes recherches. La question qui reste est pourtant celle que tout investisseur redoute : combien investir exactement ? Mettre trop peu, c’est gâcher une opportunité rare. Mettre trop, c’est risquer de tout perdre si les choses tournent mal. Cette question, qui semble relever de l’intuition ou du « feeling », possède en réalité une réponse mathématique précise. Une formule développée il y a plus de soixante ans par un ingénieur des Bell Labs, reprise ensuite par les compteurs de cartes de Las Vegas, puis adoptée par les hedge funds les plus sophistiqués de Wall Street. Cette formule s’appelle le critère de Kelly, et elle pourrait bien transformer ta façon de penser le risque et l’allocation de capital.
L’histoire du critère de Kelly commence en 1956, dans les laboratoires de recherche d’AT&T, à une époque où les mathématiques de l’information étaient en pleine effervescence. John Larry Kelly Jr., un physicien et mathématicien texan, travaillait sur un problème apparemment sans rapport avec la finance : comment optimiser la transmission de signaux sur des lignes téléphoniques bruitées. En cherchant à maximiser le débit d’information, Kelly a découvert une formule qui s’appliquait bien au-delà des télécommunications. Sa publication, intitulée « A New Interpretation of Information Rate », démontrait que la même logique mathématique pouvait déterminer la mise optimale dans un jeu de hasard. Ce qui n’était qu’une curiosité intellectuelle allait devenir l’un des outils les plus puissants de la gestion du risque moderne. Kelly lui-même n’a jamais vraiment exploité sa découverte financièrement, il est mort prématurément en 1965 à l’âge de 41 ans, mais son héritage mathématique continue d’influencer des milliards de dollars de décisions d’investissement chaque jour.
Ce qui rend le critère de Kelly fascinant, c’est qu’il résout un problème que la plupart des investisseurs ignorent même avoir. Quand on te demande combien investir dans une action prometteuse, tu penses probablement en termes de « ce que tu peux te permettre de perdre » ou de « pourcentage raisonnable de ton portefeuille ». Ces approches, bien qu’intuitivement sensées, sont mathématiquement sous-optimales. Le critère de Kelly, lui, te donne une réponse précise basée sur deux variables fondamentales : ta probabilité de gain et le rapport entre ce que tu peux gagner et ce que tu peux perdre. Le résultat est un pourcentage exact de ton capital à allouer, ni plus ni moins. Trop peu, et tu laisses de l’argent sur la table. Trop, et tu t’exposes à une ruine quasi certaine sur le long terme. Cette zone optimale, cette « sweet spot » mathématique, est ce que le critère de Kelly identifie avec une précision chirurgicale.
Avant d’entrer dans les détails de cette formule, il faut comprendre pourquoi elle n’est pas enseignée dans les cours de finance traditionnels et pourquoi elle reste relativement méconnue du grand public. La réponse tient en partie à son origine sulfureuse. Le critère de Kelly a été popularisé non pas par des professeurs d’économie, mais par des joueurs professionnels. Edward O. Thorp, mathématicien et auteur du célèbre « Beat the Dealer », a été le premier à l’appliquer systématiquement au blackjack dans les années 1960, accumulant des fortunes dans les casinos de Las Vegas avant de se tourner vers les marchés financiers. Plus tard, des légendes de l’investissement comme Warren Buffett et Charlie Munger ont reconnu utiliser des principes dérivés du critère de Kelly pour dimensionner leurs positions. La formule a donc une double vie : outil de parieurs dans les casinos, et secret bien gardé des gestionnaires de hedge funds. Cette dualité explique en partie pourquoi elle n’a jamais trouvé sa place dans les manuels de finance classiques, malgré sa puissance indéniable.
Cette newsletter va te faire découvrir le critère de Kelly sous tous ses angles. On va d’abord explorer le problème fondamental qu’il résout : pourquoi l’intuition est mauvaise conseillère pour dimensionner ses positions, et pourquoi même les investisseurs expérimentés se trompent régulièrement. Ensuite, on décortiquera la formule elle-même, avec des exemples concrets et des calculs que tu pourras reproduire chez toi avec un simple tableur. On verra comment les professionnels l’appliquent, des casinos de Vegas aux trading floors de Wall Street, en passant par les syndicats de paris sportifs asiatiques. Puis on analysera l’impact réel sur ton patrimoine, les limites à connaître, et enfin les étapes pratiques pour l’intégrer dans ta propre gestion. À la fin de cette lecture, tu auras compris quelque chose que 99 % des investisseurs ignorent : la taille de position n’est pas un détail, c’est peut-être la décision la plus importante de toute stratégie d’investissement.
Pour bien situer l’importance de ce sujet, considère les chiffres suivants. Une étude menée par Vanguard a montré que l’allocation d’actifs explique 88 % de la variance des rendements d’un portefeuille sur le long terme. Pas le stock picking, pas le market timing, pas les frais de gestion. L’allocation. Et la taille de chaque position est une composante essentielle de cette allocation. Un investisseur qui détient 50 actions mais met 40 % de son capital dans une seule d’entre elles n’est pas vraiment diversifié. Un autre qui répartit parfaitement entre 10 actions rate peut-être l’opportunité de concentrer sur ses meilleures idées. Le critère de Kelly fournit un cadre pour naviguer entre ces extrêmes, en calibrant précisément chaque position en fonction de son profil rendement-risque. C’est un outil de pilotage fin là où la plupart des investisseurs naviguent à vue.
Il y a une raison profonde pour laquelle la question du position sizing est si souvent négligée. Elle est moins sexy que la chasse aux bonnes idées d’investissement. Tout le monde veut trouver le prochain Amazon ou le prochain Bitcoin, mais personne ne veut faire des calculs de probabilités et d’écarts-types. Pourtant, trouver une bonne idée et mal l’exécuter revient souvent au même que ne pas l’avoir trouvée du tout. Imagine que tu avais identifié Tesla en 2012 comme une opportunité exceptionnelle, mais que tu n’avais mis que 0,5 % de ton portefeuille par prudence excessive. Ton gain aurait été respectable mais pas transformateur. À l’inverse, si tu avais mis 80 % de ton portefeuille, une baisse temporaire de 50 % aurait pu te faire vendre en panique au pire moment. Le critère de Kelly t’aurait donné la taille juste, ni trop ni trop peu, calibrée sur ta conviction et le profil de risque de l’investissement.
🔍 Pourquoi tu mises toujours mal (sans le savoir)
Le paradoxe de l’investisseur rationnel
Tu as probablement déjà entendu le conseil classique de diversification : ne pas mettre tous ses œufs dans le même panier. Ce conseil, bien que sage, ne répond pas à la question fondamentale. Si tu as dix opportunités d’investissement devant toi, comment répartir ton capital entre elles ? Mettre 10 % dans chacune ? Mais pourquoi 10 % et pas 15 % ou 5 % ? La diversification traditionnelle traite toutes les opportunités comme équivalentes, ce qui est rarement le cas dans la réalité. Certaines ont un meilleur rapport rendement-risque que d’autres, certaines sont quasi certaines de fonctionner, d’autres sont des paris spéculatifs. L’intuition te dit de mettre plus dans les meilleures opportunités, mais combien exactement ? C’est précisément cette question que le critère de Kelly résout avec une élégance mathématique surprenante.
Pour comprendre le problème, prenons un exemple concret qui va te faire réfléchir. Imagine un jeu de pile ou face truqué en ta faveur : à chaque lancer, tu as 60 % de chances de gagner. Quand tu gagnes, tu doubles ta mise. Quand tu perds, tu perds ta mise. C’est un jeu manifestement favorable, avec une espérance positive. La question est : quelle fraction de ta fortune dois-tu miser à chaque tour pour maximiser ta richesse sur le long terme ? L’intuition naïve pourrait te pousser à miser 100 % à chaque fois, puisque le jeu est en ta faveur. Mais cette stratégie te conduit à la ruine quasi certaine : il suffit d’une seule perte pour tout perdre. À l’opposé, miser seulement 1 % à chaque tour est trop conservateur et ne tire pas pleinement parti de ton avantage. Entre ces deux extrêmes, il existe une fraction optimale, et c’est exactement ce que le critère de Kelly calcule.
Le problème devient encore plus subtil quand on considère la dynamique temporelle de l’investissement. Ce qui compte n’est pas seulement l’espérance de gain à chaque transaction, mais la croissance composée de ton capital sur des centaines ou des milliers de transactions. Un investisseur qui mise trop gros peut avoir une espérance positive à chaque trade, mais voir son capital s’effondrer sur le long terme à cause de la volatilité. C’est ce qu’on appelle le risque de ruine, un concept souvent négligé dans l’enseignement classique de la finance. Le critère de Kelly intègre naturellement ce risque dans son calcul, car il optimise non pas l’espérance arithmétique des gains, mais leur espérance géométrique, c’est-à-dire le taux de croissance composé du capital. Cette distinction technique a des conséquences pratiques massives.
Pour illustrer ce point de manière frappante, considérons deux investisseurs qui jouent au même jeu favorable pendant 100 tours. L’investisseur A mise 50 % de son capital à chaque tour, convaincu de maximiser ses gains puisque le jeu est en sa faveur. L’investisseur B mise 20 % de son capital, conformément au critère de Kelly. Après 100 tours, les simulations montrent un résultat contre-intuitif : l’investisseur A a probablement perdu la majeure partie de son capital initial, malgré un jeu en sa faveur, tandis que l’investisseur B a multiplié sa mise initiale par un facteur impressionnant, souvent plusieurs milliers. Ce n’est pas de la magie, c’est la différence entre optimiser pour l’espérance arithmétique (ce que fait intuitivement l’investisseur A) et optimiser pour l’espérance géométrique (ce que fait le critère de Kelly). Cette distinction subtile mais cruciale est au cœur de tout ce qui va suivre.
Ce phénomène a été vérifié empiriquement dans de nombreux contextes. Dans les années 1980, des chercheurs de l’université de Chicago ont organisé une expérience où des participants devaient jouer à un jeu favorable (60 % de chances de gagner, gain égal à la mise). Malgré les instructions claires sur les probabilités, plus de 30 % des participants ont fait faillite avant la fin de l’expérience, simplement parce qu’ils misaient trop gros. Les participants qui ont survécu et prospéré étaient ceux qui, consciemment ou non, misaient des fractions proches du Kelly optimal. Cette expérience démontre que même des personnes intelligentes et informées peuvent se ruiner sur des jeux favorables par manque de discipline dans le position sizing.
Pourquoi l’espérance ne suffit pas
L’un des concepts les plus contre-intuitifs de la gestion du risque est la différence entre moyenne arithmétique et moyenne géométrique. Prenons un exemple simple. Tu investis 100 € dans un actif qui fait +50 % la première année, puis -50 % la deuxième année. Arithmétiquement, la performance moyenne est de 0 % par an : (+50 % - 50 %) / 2 = 0 %. Pourtant, après ces deux années, tu n’as plus que 75 € : 100 × 1,5 × 0,5 = 75. Ta vraie performance, celle qui compte pour ton patrimoine, est négative : environ -13 % au total, soit -6,7 % par an en composé. C’est la moyenne géométrique qui reflète la réalité : le taux de croissance composé de ton capital. Cette distinction est fondamentale pour comprendre pourquoi miser gros sur des opportunités volatiles peut être désastreux, même quand l’espérance est positive.
Ce phénomène porte un nom technique : la volatility drag, ou « traînée de volatilité ». Plus un investissement est volatile, plus l’écart entre sa moyenne arithmétique et sa moyenne géométrique se creuse. C’est pourquoi un actif qui fait +100 % puis -50 % te laisse exactement au point de départ (100 × 2 × 0,5 = 100), alors que sa performance arithmétique moyenne est de +25 %. Ce n’est pas une anomalie mathématique, c’est la réalité de comment fonctionne la croissance composée. Le critère de Kelly prend en compte cette réalité en maximisant directement la moyenne géométrique, c’est-à-dire le taux de croissance à long terme de ton patrimoine. C’est ce qui le distingue des approches naïves basées uniquement sur l’espérance de gain.
Pour illustrer concrètement cette différence, imaginons deux stratégies d’investissement appliquées sur le même jeu favorable. La stratégie A mise 25 % du capital à chaque opportunité, tandis que la stratégie B mise 75 %. Les deux jouent le même jeu avec 60 % de chances de doubler la mise et 40 % de chances de tout perdre. Sur une seule transaction, la stratégie B a une espérance plus élevée : 0,6 × 75 % - 0,4 × 75 % = 15 % contre 0,6 × 25 % - 0,4 × 25 % = 5 % pour la stratégie A. Mais sur 100 transactions, la stratégie A aura multiplié le capital initial par un facteur gigantesque, tandis que la stratégie B aura probablement été ruinée plusieurs fois. Ce résultat, apparemment paradoxal, découle directement de la différence entre moyennes arithmétique et géométrique. Le critère de Kelly, dans ce cas précis, recommanderait une mise d’environ 20 % du capital, légèrement inférieure à la stratégie A.
Cette réalité mathématique explique pourquoi tant d’investisseurs particuliers, pourtant intelligents et informés, finissent par sous-performer le marché sur le long terme. Ils tombent dans le piège de la volatilité : attirés par les actifs qui promettent les plus hauts rendements, ils négligent l’impact dévastateur de la volatilité sur la croissance composée. Un fonds qui fait +40 % une année, -30 % l’année suivante, +50 %, puis -25 % affiche une moyenne arithmétique de +8,75 % par an. Impressionnant sur le papier. Sauf que ton capital réel a à peine bougé : 100 × 1,4 × 0,7 × 1,5 × 0,75 = 110,25, soit un rendement composé de seulement 2,5 % par an sur quatre ans. La différence entre 8,75 % et 2,5 % sur 30 ans de carrière d’investisseur, c’est la différence entre finir millionnaire et finir avec un patrimoine modeste. Le critère de Kelly te protège contre cette illusion en optimisant ce qui compte vraiment : la croissance géométrique.
Le mythe du money management intuitif
La plupart des investisseurs particuliers, et même beaucoup de professionnels, gèrent la taille de leurs positions de manière intuitive. Ils se fixent des règles empiriques comme « ne jamais mettre plus de 5 % dans une seule action » ou « limiter les pertes à 2 % du portefeuille par trade ». Ces règles, bien que prudentes, sont complètement arbitraires d’un point de vue mathématique. Pourquoi 5 % et pas 7 % ? Pourquoi 2 % et pas 3 % ? Ces chiffres ronds ne correspondent à aucune optimisation rigoureuse. Ils sont choisis parce qu’ils « semblent raisonnables » ou parce qu’un gourou de la finance les a recommandés dans un livre à succès. Le problème est que ce qui semble raisonnable peut être soit trop conservateur, soit dangereusement agressif selon les caractéristiques de chaque opportunité.
Un autre mythe répandu est celui de la gestion du risque par le stop-loss. L’idée est de placer un ordre de vente automatique qui limite les pertes à un pourcentage prédéfini, par exemple -10 %. Cette technique, bien que psychologiquement rassurante, ne résout pas le problème fondamental de la taille de position. Un stop-loss à -10 % sur une position de 50 % du portefeuille représente une perte de 5 % du capital total. Le même stop-loss sur une position de 10 % ne représente que 1 % du capital. La vraie question reste : quelle taille de position est optimale compte tenu de la probabilité que le stop-loss soit touché et du gain potentiel si le trade fonctionne ? Le critère de Kelly intègre ces paramètres dans un calcul unique et cohérent, là où le stop-loss ne traite qu’une partie du problème.
La gestion intuitive du risque souffre également d’un biais cognitif bien documenté : l’aversion aux pertes. Les études en économie comportementale, notamment celles de Daniel Kahneman et Amos Tversky, montrent que la douleur d’une perte est ressentie environ deux fois plus intensément que le plaisir d’un gain équivalent. Ce biais pousse naturellement les investisseurs à sous-dimensionner leurs positions, même quand l’opportunité est excellente. « Je préfère ne pas risquer trop » devient un mantra qui coûte cher sur le long terme. À l’inverse, après une série de gains, l’excès de confiance peut pousser à surdimensionner les positions au pire moment. Le critère de Kelly offre un antidote à ces biais en fournissant une réponse objective et calculée, indépendante de l’état émotionnel du moment. Ce n’est pas une garantie de succès, mais c’est un garde-fou contre les décisions irrationnelles.
Les professionnels de la gestion d’actifs ne sont pas épargnés par ces travers. Une étude célèbre menée par Odean et Barber a montré que les investisseurs individuels qui tradent le plus fréquemment sont aussi ceux qui performent le moins bien, en grande partie parce qu’ils surdimensionnent leurs positions et multiplient les frais de transaction. Les fonds de gestion active, malgré leurs équipes d’analystes et leurs modèles sophistiqués, sous-performent majoritairement les indices passifs sur le long terme. Une partie de cette sous-performance s’explique par des erreurs de position sizing : trop de diversification sur des idées médiocres, pas assez de concentration sur les meilleures convictions. Le critère de Kelly, en théorie, résout exactement ce problème. En pratique, très peu de gestionnaires l’appliquent rigoureusement, pour des raisons que nous allons explorer.
Un phénomène particulièrement révélateur est celui du career risk dans l’industrie de la gestion d’actifs. Un gérant de fonds qui sous-performe pendant trois ans risque de perdre son emploi, même si sa stratégie est mathématiquement optimale sur le long terme. Ce risque professionnel pousse les gérants à « serrer le benchmark », c’est-à-dire à construire des portefeuilles qui ressemblent fortement à l’indice de référence. Cette stratégie minimise le risque de sous-performance catastrophique, mais elle garantit aussi une sous-performance modérée après frais. Le critère de Kelly, lui, encourage la prise de positions concentrées quand l’avantage le justifie, ce qui est l’inverse de ce que les incitations de carrière recommandent. C’est une des raisons pour lesquelles les hedge funds indépendants, où les gérants ont leur propre argent en jeu, sont souvent plus proches des principes Kelly.
La notion de risque de carrière n’affecte pas que les professionnels. Toi aussi, en tant qu’investisseur particulier, tu fais face à des pressions sociales qui peuvent fausser tes décisions. Si tu mises gros sur une action et qu’elle chute de 40 %, tu vas devoir expliquer ta décision à ton conjoint, peut-être à tes amis qui investissent. Cette perspective désagréable peut te pousser inconsciemment vers des positions trop petites, même quand l’opportunité est excellente. Le critère de Kelly, en fournissant une justification mathématique à la taille de position, peut servir de bouclier contre ces pressions. « J’ai calculé le Kelly, et il recommande 15 % » est une réponse plus solide que « j’ai mis ce qui me semblait raisonnable ». La formule devient alors un outil de communication autant qu’un outil de décision.
📊 L’équation qui tient sur un post-it
L’équation originale de Kelly
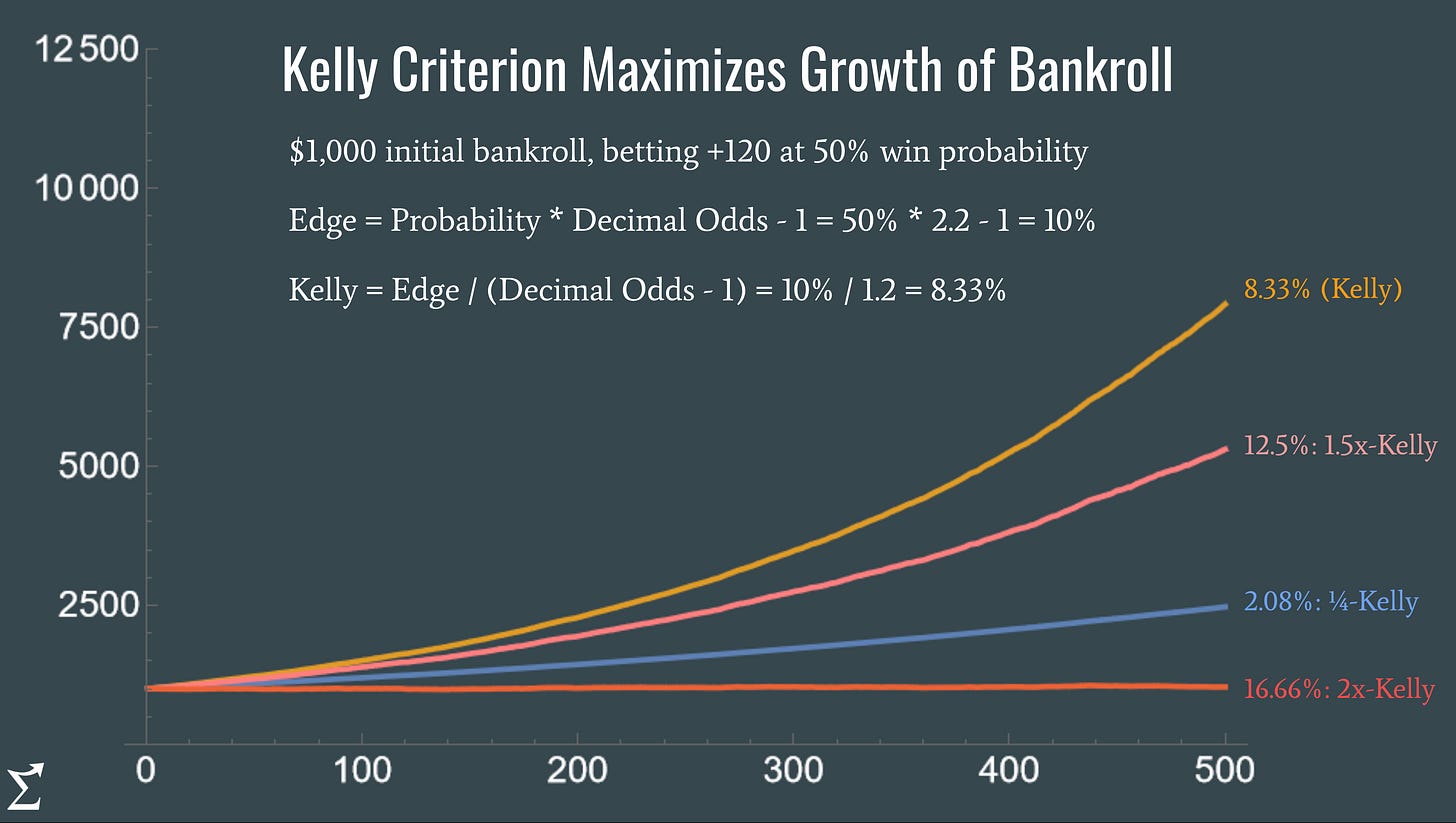
Le critère de Kelly, dans sa forme la plus simple, s’exprime par une équation d’une élégance remarquable. Pour un pari binaire où tu as une probabilité p de gagner et une probabilité q = 1 - p de perdre, avec un gain de b fois ta mise en cas de victoire et une perte totale de ta mise en cas de défaite, la fraction optimale de ton capital à miser est : **f* = (bp - q) / b. Cette formule peut se réécrire de manière plus intuitive comme f* = p - q/b**, où p est ta probabilité de gain, q ta probabilité de perte, et b le ratio de gain. Par exemple, si tu as 60 % de chances de gagner (p = 0,6) et que tu doubles ta mise en cas de victoire (b = 1), alors f* = 0,6 - 0,4/1 = 0,2, soit 20 % de ton capital. Cette fraction optimale s’appelle la fraction de Kelly ou simplement « Kelly ».
Pour comprendre intuitivement cette formule, décomposons-la étape par étape. Le terme bp représente l’espérance de gain : c’est le gain potentiel (b) multiplié par la probabilité de l’obtenir (p). Le terme q représente l’espérance de perte : c’est la perte potentielle (1, soit 100 % de la mise) multipliée par la probabilité de perdre (q). La différence bp - q est donc l’avantage net que tu as sur chaque pari, exprimé en unités de mise. Si cette différence est négative, la formule te dit de ne pas miser du tout, ce qui est logique puisque le jeu est défavorable. Si elle est positive, la formule divise cet avantage par b pour déterminer quelle fraction du capital mobiliser. Plus ton avantage est grand, plus tu peux miser. Plus le gain potentiel est élevé (grand b), moins tu as besoin de miser gros pour capitaliser sur ton avantage.
Prenons quelques exemples concrets pour ancrer cette formule dans la réalité. Premier cas : un investissement avec 55 % de chances de gagner 20 % et 45 % de chances de perdre 10 %. En traduisant dans les termes de Kelly, p = 0,55, q = 0,45, et b = 2 (tu gagnes 2 fois ce que tu risques, puisque 20 % de gain pour 10 % de risque). La fraction optimale est f* = (2 × 0,55 - 0,45) / 2 = 0,65 / 2 = 32,5 %. Deuxième cas : un pari plus risqué avec 40 % de chances de tripler ta mise et 60 % de chances de tout perdre. Ici p = 0,4, q = 0,6, b = 2 (gain net de 200 %, donc b = 2). La formule donne f* = (2 × 0,4 - 0,6) / 2 = 0,2 / 2 = 10 %. Remarque comment le critère de Kelly recommande une mise beaucoup plus faible pour le second cas, bien que le gain potentiel soit plus élevé, parce que la probabilité de succès est plus basse.
Un troisième exemple montre ce qui se passe quand le jeu est défavorable. Imagine un pari avec 40 % de chances de gagner et des cotes de 1 contre 1 (tu doubles ta mise ou tu perds tout). Les paramètres sont p = 0,4, q = 0,6, b = 1. Le Kelly donne f* = (1 × 0,4 - 0,6) / 1 = -0,2. Une fraction négative signifie que tu ne devrais pas miser du tout, voire parier contre si c’était possible. C’est exactement ce qu’on attend d’une formule rationnelle : elle refuse de t’engager dans des jeux perdants. Cette propriété distingue le critère de Kelly des approches purement psychologiques où un investisseur pourrait quand même « tenter le coup » sur un mauvais pari, influencé par l’espoir ou l’ennui.
Un quatrième exemple particulièrement instructif concerne les opportunités à très fort potentiel. Imagine que tu aies 30 % de chances de faire fois 10 sur ta mise (b = 9) et 70 % de chances de tout perdre. L’espérance est positive : 0,3 × 9 - 0,7 × 1 = 2,7 - 0,7 = 2, soit un gain moyen de 200 % par pari. Pourtant, le Kelly recommande f* = (9 × 0,3 - 0,7) / 9 = 2 / 9 = 22 %. Malgré une espérance énorme, la mise recommandée reste modérée. Pourquoi ? Parce que la probabilité de perte de 70 % signifie que tu vas perdre plus souvent que tu vas gagner. Miser trop gros te conduirait à la ruine avant que ton avantage ne se manifeste. Le Kelly équilibre parfaitement l’appât du gain et la prudence face au risque.
La version généralisée pour les investissements
La formule originale de Kelly suppose un pari binaire : soit tu gagnes b fois ta mise, soit tu perds tout. Cette hypothèse est trop simpliste pour la plupart des investissements réels, où les résultats possibles forment un continuum. Heureusement, le critère de Kelly peut être généralisé pour tenir compte de distributions de rendements plus complexes. Pour un investissement avec un rendement espéré μ (mu) et une variance σ² (sigma carré), la fraction de Kelly approximative est : **f* = μ / σ²**. Cette formule, parfois appelée le critère de Kelly-Merton du nom de l’économiste Robert Merton qui l’a formalisée, est utilisée par les gestionnaires de portefeuille pour dimensionner leurs positions sur les marchés financiers. Elle dit essentiellement que tu devrais investir proportionnellement au rendement espéré et inversement proportionnellement au risque mesuré par la variance.
Cette version généralisée révèle une propriété importante du critère de Kelly : il pénalise fortement la volatilité. Un investissement avec un rendement espéré de 10 % et une volatilité de 20 % justifie une allocation de 10 % / (20 %)² = 10 % / 4 % = 2,5 fois le capital, ce qui n’a pas de sens pratique sans levier. En réalité, cette formule suppose une capacité d’emprunt illimitée au taux sans risque, ce qui n’est pas réaliste pour un particulier. Pour un investisseur sans accès au levier, le résultat doit être plafonné à 100 %. Le même calcul avec une volatilité de 40 % donne 10 % / 16 % = 62,5 % du capital, une allocation déjà plus raisonnable. La leçon est claire : à rendement espéré égal, le critère de Kelly recommande d’investir beaucoup moins dans les actifs volatils.
Pour les investisseurs en actions, une application pratique consiste à utiliser le ratio de Sharpe comme point de départ. Le ratio de Sharpe mesure le rendement excédentaire (au-delà du taux sans risque) divisé par la volatilité. Si un investissement a un ratio de Sharpe de 0,5 et une volatilité de 25 %, le critère de Kelly suggère une allocation d’environ 0,5 × 0,25 = 12,5 % du portefeuille. Cette règle simple permet d’ajuster rapidement la taille de position en fonction du profil rendement-risque de chaque opportunité. Un actif avec un excellent ratio de Sharpe de 1,0 et une faible volatilité de 15 % justifierait une allocation de 1,0 × 0,15 = 15 %, tandis qu’un actif spéculatif avec un ratio de Sharpe de 0,3 et une volatilité de 50 % ne justifierait que 0,3 × 0,5 = 15 % également, mais avec un profil de risque très différent.
Une autre extension utile concerne les paris à pertes partielles. Dans la vie réelle, tu ne perds pas toujours 100 % de ta mise quand un investissement tourne mal. Si tu achètes une action et qu’elle baisse de 20 % avant que tu vendes, tu as perdu 20 %, pas 100 %. Le critère de Kelly peut être ajusté pour ces situations en introduisant un paramètre de perte partielle l. Si tu gagnes b fois ta mise avec probabilité p, et tu perds une fraction l de ta mise avec probabilité q, la formule devient **f* = (bp - ql) / bl**. Cette version plus réaliste produit généralement des Kelly plus élevés que la version binaire, car le risque est atténué par les pertes partielles. Elle est particulièrement pertinente pour l’investissement en actions, où les pertes totales sont heureusement rares pour des entreprises établies.
Le fractional Kelly : la prudence mathématique
Dans la pratique, très peu d’investisseurs professionnels utilisent le critère de Kelly à 100 %. La raison est double et importante à comprendre. D’abord, les paramètres de la formule (probabilités de gain, ratios de rendement) sont estimés, pas connus avec certitude. Toute erreur d’estimation dans un sens optimiste conduira à surmiser dangereusement. Ensuite, même avec des paramètres parfaitement connus, le critère de Kelly produit une volatilité de portefeuille très élevée que peu d’investisseurs peuvent tolérer psychologiquement. La solution universellement adoptée est le fractional Kelly : au lieu de miser la fraction optimale f*, on mise une fraction de cette fraction, typiquement entre 25 % et 50 %. Autrement dit, si Kelly recommande 20 %, on mise entre 5 % et 10 %. Cette approche conservatrice sacrifie un peu de rendement espéré pour une réduction substantielle de la volatilité et une marge de sécurité contre les erreurs.
Les avantages du fractional Kelly sont multiples et bien documentés par la recherche académique. Premièrement, il offre une marge de sécurité contre les erreurs d’estimation. Si tu te trompes de 50 % sur ta probabilité de gain, un Kelly complet pourrait te mener à la ruine, alors qu’un demi-Kelly ne fera que réduire ton rendement sans catastrophe. Deuxièmement, le fractional Kelly produit un parcours de richesse plus régulier. Les simulations de Monte Carlo montrent qu’un demi-Kelly atteint environ 75 % du rendement du Kelly complet avec seulement 50 % de sa volatilité. Ce compromis est très attractif pour la plupart des investisseurs. Troisièmement, le fractional Kelly laisse une réserve de capital pour saisir de nouvelles opportunités. Un portefeuille en Kelly complet est toujours investi au maximum, sans marge de manœuvre pour les bonnes surprises.
Edward Thorp, le mathématicien qui a popularisé le critère de Kelly et l’a appliqué avec succès pendant des décennies, a lui-même déclaré utiliser systématiquement un demi-Kelly ou moins dans ses investissements. Sa logique était simple et éloquente : « Les conséquences de surmiser sont bien pires que celles de sous-miser. » Si tu mises le double du Kelly optimal, ton taux de croissance devient nul, et tu subis une volatilité insoutenable sans aucun gain à long terme. Si tu mises la moitié du Kelly optimal, tu conserves 75 % du taux de croissance avec beaucoup moins de stress. Ce constat asymétrique justifie une approche conservatrice. Concrètement, pour un investisseur particulier, la règle pratique est de calculer la fraction de Kelly puis de la diviser par deux, voire par quatre pour les paris très incertains. C’est cette version prudente qui est réellement utilisable au quotidien.
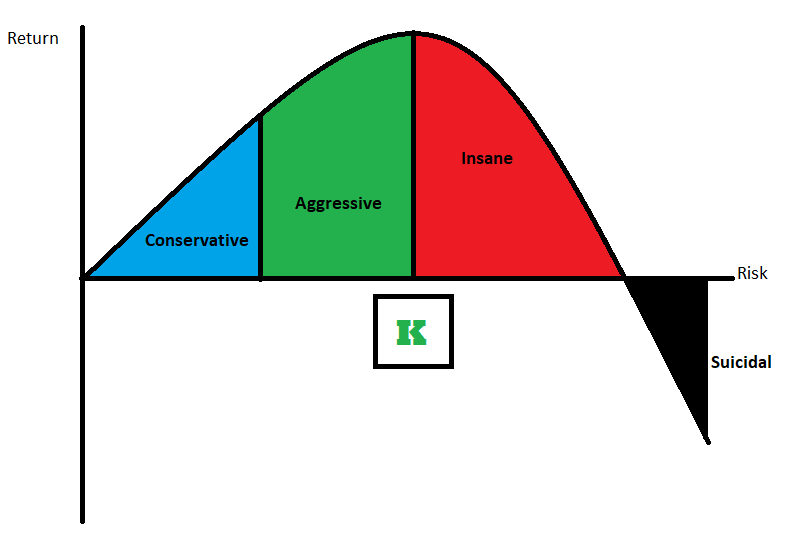
Pour bien comprendre cette asymétrie cruciale, imaginons un graphique du taux de croissance en fonction de la fraction misée. Le taux de croissance est nul à 0 % (tu ne mises rien, tu ne gagnes rien), maximal au Kelly optimal, et à nouveau nul au double du Kelly. Au-delà du double, le taux de croissance devient négatif : tu perds de l’argent en moyenne sur le long terme, même avec un avantage positif à chaque pari. Cette courbe en cloche explique pourquoi sous-miser est toujours préférable à surmiser. Si tu mises la moitié du Kelly, tu es sur la pente montante de la courbe, avec un rendement positif et confortable. Si tu mises le double, tu es au sommet retombant avec un rendement nul malgré tes efforts. Et si tu mises plus du double, tu es en territoire négatif où chaque pari te rapproche de la ruine. Face à l’incertitude sur le vrai Kelly optimal, la prudence commande de viser bas plutôt que haut.
🔎 Les milliardaires qui misent avec une calculette
Des casinos aux hedge funds
L’histoire de l’application du critère de Kelly aux marchés financiers commence avec Edward O. Thorp dans les années 1960, et c’est une histoire fascinante de génie mathématique appliqué. Après avoir développé la première stratégie de comptage de cartes au blackjack et démontré qu’il était possible de battre les casinos de manière systématique, Thorp a tourné son attention vers un « casino » encore plus grand et plus lucratif : Wall Street. En 1967, il publie « Beat the Market » avec Sheen Kassouf, un livre révolutionnaire qui applique les méthodes quantitatives au trading de warrants et d’options, identifiant des anomalies de prix que le marché n’avait pas encore corrigées. En 1969, il fonde Princeton Newport Partners, l’un des premiers hedge funds quantitatifs de l’histoire, qui générera des rendements de 20 % par an pendant près de deux décennies avec une volatilité remarquablement faible. Le secret de cette performance ? Une application rigoureuse du critère de Kelly pour dimensionner chaque position.
Le fonds de Thorp n’était pas le seul à utiliser ces principes, mais il a ouvert la voie à toute une industrie. Jim Simons, fondateur de Renaissance Technologies et du légendaire fonds Medallion, est un autre adepte bien connu des méthodes probabilistes de gestion du risque. Medallion, considéré comme le hedge fund le plus performant de l’histoire avec des rendements annuels de plus de 60 % avant frais depuis 1988, utilise des algorithmes sophistiqués pour estimer les probabilités de succès de milliers de trades quotidiens. Bien que les détails de leurs modèles soient gardés secrets comme des recettes de Coca-Cola, les anciens employés ont confirmé que le dimensionnement des positions basé sur des principes dérivés de Kelly est au cœur de leur stratégie. La fortune personnelle de Simons, estimée à plus de 25 milliards de dollars, témoigne de l’efficacité de ces méthodes sur le long terme.
Plus proche de l’investisseur particulier en termes de style, Warren Buffett a également reconnu l’influence du critère de Kelly sur sa philosophie d’investissement, bien qu’il ne l’applique pas de manière mathématique formelle avec des tableurs et des formules. Dans ses lettres aux actionnaires de Berkshire Hathaway, Buffett insiste régulièrement sur l’importance de concentrer le portefeuille sur les meilleures idées plutôt que de diversifier à l’excès dans des dizaines de positions médiocres. Sa célèbre citation « La diversification est une protection contre l’ignorance. Elle n’a guère de sens pour ceux qui savent ce qu’ils font » reflète cette philosophie Kelly. Charlie Munger, son partenaire de longue date, a explicitement mentionné le critère de Kelly dans plusieurs interviews, expliquant qu’il justifie de miser gros quand on a un avantage informationnel significatif et qu’on comprend vraiment ce qu’on achète.
Un cas d’étude particulièrement instructif est celui de Bill Gross, le « roi des obligations » qui a régné sur les marchés obligataires pendant des décennies. Pendant son règne chez PIMCO, Gross a géré le plus grand fonds obligataire du monde, accumulant des performances exceptionnelles année après année. Dans son autobiographie et ses interviews, il révèle utiliser une version modifiée du critère de Kelly pour dimensionner ses paris directionnels sur les taux d’intérêt. Quand il estimait avoir un avantage significatif (par exemple, en prédisant correctement la politique de la Fed avant le marché), il augmentait massivement ses positions. Quand l’incertitude était élevée, il réduisait son exposition au minimum. Cette discipline systématique, combinée à une expertise profonde des marchés obligataires acquise sur des décennies, explique en grande partie sa surperformance durable.
Application aux paris sportifs et au poker
Les paris sportifs professionnels constituent l’un des terrains d’application les plus directs et les plus purs du critère de Kelly. Un parieur professionnel estime la probabilité réelle d’un événement sportif (par exemple, 55 % de chances que l’équipe A gagne le match) et la compare à la cote offerte par le bookmaker. Si la cote implique une probabilité de seulement 45 %, le parieur a un avantage (edge en anglais) de 10 points de pourcentage. Le critère de Kelly lui dit alors exactement quelle fraction de sa bankroll parier pour maximiser sa croissance à long terme. Cette approche disciplinée et mathématique est ce qui distingue les parieurs professionnels rentables des amateurs qui misent au feeling, à l’émotion, ou selon leurs équipes préférées. Les syndicats de paris les plus sophistiqués utilisent des équipes d’analystes et des modèles statistiques avancés pour estimer les probabilités, puis appliquent systématiquement le fractional Kelly pour dimensionner leurs mises.
Au poker, l’application du critère de Kelly est plus nuancée mais tout aussi pertinente pour les joueurs sérieux. Contrairement aux paris sportifs où chaque pari est indépendant, le poker implique des décisions séquentielles avec information incomplète et une dimension psychologique importante. Cependant, la question du bankroll management — combien de buy-ins maintenir pour jouer à un certain niveau — peut être analysée avec des principes dérivés de Kelly. Un joueur de poker professionnel sait que même avec un avantage significatif sur ses adversaires, la variance du jeu peut produire de longues séries de pertes appelées « downswings ». Le critère de Kelly, adapté au contexte du poker, suggère de maintenir suffisamment de buy-ins pour survivre aux inévitables périodes difficiles tout en montant de niveau quand la bankroll le permet. Les recommandations classiques de 20 à 30 buy-ins pour le cash game correspondent grossièrement à un fractional Kelly conservateur.
Un exemple concret illustre bien la puissance de cette approche dans les paris sportifs. Imagine un parieur qui découvre que le bookmaker sous-estime systématiquement les performances d’une équipe de basketball universitaire qu’il connaît très bien. Son modèle statistique, affiné sur plusieurs saisons, lui donne un avantage moyen de 3 % par pari. Avec des cotes de l’ordre de 2,0 (gain égal à la mise), le critère de Kelly recommande une mise d’environ 3 % / 1 = 3 % de la bankroll par pari. Avec un demi-Kelly conservateur, ce serait 1,5 % par pari. Sur 500 paris dans une saison, avec un avantage réel de 3 %, la bankroll initiale de 10 000 € pourrait croître jusqu’à environ 25 000 € en Kelly complet ou 18 000 € en demi-Kelly. La différence de volatilité est massive : le Kelly complet pourrait voir des drawdowns de 50 % en cours de route, tandis que le demi-Kelly limiterait les pertes maximales à environ 25 %. Pour la plupart des parieurs, le confort psychologique du demi-Kelly vaut largement le sacrifice de rendement final.
Les syndicats de paris asiatiques, réputés pour être les opérateurs les plus sophistiqués et les mieux capitalisés du marché mondial, sont connus pour utiliser des versions avancées du critère de Kelly intégrant les corrélations entre paris et l’évolution dynamique des cotes. Quand un syndicat place un gros pari, les bookmakers ajustent leurs cotes presque instantanément, réduisant l’avantage pour les paris suivants sur le même événement. Le Kelly dynamique prend en compte cet effet en réduisant la taille des paris à mesure que l’avantage s’érode. Ces opérateurs traitent les paris sportifs exactement comme un hedge fund traite les marchés financiers : avec des modèles quantitatifs, une gestion du risque rigoureuse, et une discipline de fer. Le critère de Kelly est leur colonne vertébrale, mais ils l’entourent de nombreuses sophistications pratiques développées au fil des décennies d’expérience.
Et pour l’investisseur particulier ?
L’investisseur particulier fait face à un défi que les hedge funds et les parieurs professionnels n’ont pas dans la même mesure : l’impossibilité de quantifier précisément son avantage. Quand tu achètes des actions Apple, quelle est ta probabilité de surperformer le marché ? 51 % ? 55 % ? 60 % ? La réponse honnête est que tu n’en sais probablement rien avec précision. Cette incertitude fondamentale rend l’application stricte du critère de Kelly problématique pour l’investisseur lambda. Cependant, les principes sous-jacents restent précieux et applicables. Le critère de Kelly enseigne que la taille de position doit être proportionnelle à ton avantage et inversement proportionnelle au risque. Même sans chiffres précis, cette logique peut guider tes décisions : plus tu es confiant dans une opportunité et plus tu comprends l’entreprise, plus tu peux allouer de capital, mais jamais au point de risquer la ruine.
Une application pratique pour l’investisseur particulier est la distinction entre le cœur de portefeuille et les positions satellites. Le cœur, typiquement composé d’ETF diversifiés sur lesquels tu n’as aucun avantage particulier par rapport au marché, devrait représenter la majorité du portefeuille (60 à 80 % selon ton profil). Les positions satellites, où tu penses avoir un avantage (connaissance approfondie d’un secteur, conviction forte sur une entreprise, timing opportun identifié), peuvent être dimensionnées selon une version simplifiée du critère de Kelly. Si tu es très confiant (disons 70 % de chances de surperformer de 20 %), tu peux allouer davantage. Si tu es moins sûr (55 % de chances de surperformer de 10 %), tu alloues moins. Cette approche semi-quantitative est plus rigoureuse que le pur instinct sans être aussi exigeante que le Kelly mathématique des professionnels.
Un dernier point crucial concerne la corrélation entre les positions, souvent ignorée par les investisseurs particuliers. Le critère de Kelly classique suppose des paris indépendants, ce qui n’est jamais le cas sur les marchés financiers. Si tu as cinq positions dans cinq entreprises tech différentes (Apple, Microsoft, Google, Amazon, Meta), elles vont toutes monter ou baisser ensemble dans une large mesure car elles sont exposées aux mêmes facteurs macroéconomiques. Le Kelly optimal pour le portefeuille global est donc inférieur à la somme des Kelly individuels calculés séparément. En pratique, cela signifie que même si chaque position semble justifier 10 % du portefeuille selon Kelly, le total ne devrait pas dépasser 30 ou 40 % si les positions sont corrélées. Cette réalité renforce l’argument en faveur du fractional Kelly : mieux vaut être trop prudent que de découvrir trop tard que tes « positions diversifiées » étaient en fait un seul gros pari déguisé en cinq.
Pour l’investisseur qui souhaite aller plus loin dans l’application du Kelly, des outils en ligne permettent de calculer le Kelly pour des portefeuilles de plusieurs actifs corrélés. Ces calculateurs demandent en entrée les rendements espérés, les volatilités, et la matrice de corrélation entre actifs. Le résultat est un vecteur d’allocations optimales qui tient compte des interactions entre positions. Cette approche est évidemment plus sophistiquée que le Kelly simple, mais elle reste accessible à quiconque maîtrise un tableur Excel ou Google Sheets. Le site d’Edward Thorp lui-même propose des ressources pédagogiques sur ce sujet, et plusieurs universités ont publié des études détaillant les formules et les implémentations pratiques du Kelly multi-actifs pour les lecteurs qui veulent approfondir.
Un cas d’application particulièrement intéressant pour les investisseurs systématiques est celui des stratégies momentum, très populaires parmi les investisseurs qui suivent des règles quantitatives. Ces stratégies consistent à acheter les actifs qui ont le plus monté récemment et à vendre ceux qui ont le plus baissé, surfant sur la persistance des tendances. Le momentum est l’un des facteurs de performance les plus robustes dans la recherche académique en finance, mais il souffre de drawdowns importants et de « momentum crashes » occasionnels quand les tendances s’inversent brutalement. Le critère de Kelly peut aider à calibrer l’exposition au momentum en fonction de la force du signal. Quand le momentum est fort (grandes différences de performance entre gagnants et perdants), le Kelly suggère une exposition plus élevée. Quand le momentum est faible ou ambigu, il recommande de réduire les positions.
Les stratégies de valeur offrent un autre terrain d’application naturel pour le Kelly. Un investisseur value cherche des actions sous-évaluées par rapport à leurs fondamentaux (bénéfices, actifs, cash-flows). Quand une action est très sous-évaluée selon de multiples métriques concordantes, le Kelly suggère une position plus importante car la marge de sécurité est élevée. Quand la sous-évaluation est modeste ou incertaine (une seule métrique favorable, d’autres ambiguës), le Kelly recommande une position plus petite. Cette discipline aide à résister à la tentation de mettre trop dans une action « en apparence bon marché » qui pourrait être un piège de valeur (value trap). Le critère de Kelly force à expliciter : quelle est vraiment ma probabilité de surperformer ? Quel est vraiment mon ratio rendement/risque ? Ces questions révèlent souvent que l’opportunité est moins attractive qu’elle n’y paraît au premier abord.
L’application du Kelly aux cryptomonnaies mérite également une mention, car c’est un terrain où beaucoup d’investisseurs particuliers font des erreurs massives de position sizing. La volatilité extrême des cryptos (routinièrement 50-80 % de drawdown) signifie que le Kelly recommande des positions beaucoup plus faibles que pour des actions traditionnelles, même si l’espérance de rendement semble élevée. Un investisseur qui met 30 % de son portefeuille en Bitcoin parce qu’il « croit au potentiel » viole probablement le Kelly de manière spectaculaire. Avec une volatilité annualisée de 80 % et un rendement espéré optimiste de 30 %, le Kelly suggère une allocation d’environ 30 % / 64 % = 47 %, et avec un demi-Kelly prudent, seulement 23 %. Beaucoup d’investisseurs crypto sont massivement surdimensionnés par rapport à ce que les mathématiques recommandent.
💥 Survivre ou performer : le vrai choix
La différence entre croître et survivre
Le critère de Kelly révèle une vérité fondamentale sur l’investissement à long terme : survivre est plus important que performer. Cette affirmation peut sembler contre-intuitive dans un monde obsédé par les rendements et les classements de performance, mais elle découle directement des mathématiques de la croissance composée. Un investisseur qui fait +20 % par an pendant 20 ans puis perd 100 % la vingt-et-unième année finit avec zéro, exactement comme s’il n’avait jamais investi du tout. Un investisseur qui fait +10 % par an pendant 21 ans, soit deux fois moins à chaque période, finit avec plus du double de sa mise initiale (environ 7,4 fois). La leçon est claire et implacable : les grands coups ne servent à rien si tu ne survis pas pour en profiter. Le critère de Kelly intègre cette réalité en maximisant le taux de croissance tout en éliminant mathématiquement le risque de ruine.
Cette perspective a des implications profondes pour la construction de portefeuille. Les stratégies qui promettent des rendements spectaculaires avec un risque de perte totale, même faible en apparence, sont mathématiquement inférieures aux stratégies plus conservatrices sur le long terme. C’est pourquoi les professionnels expérimentés évitent généralement les produits à effet de levier extrême, les options binaires, et les investissements concentrés dans des actifs hautement spéculatifs. Nassim Taleb, l’auteur du « Cygne Noir » et lui-même ancien trader d’options, résume cette idée par sa stratégie de « barbell » : combiner des actifs très sûrs (pour survivre quoi qu’il arrive) avec de petites positions spéculatives (pour profiter des gains asymétriques), en évitant le milieu du spectre où le risque semble modéré mais peut s’avérer catastrophique lors des crises.
Les simulations de Monte Carlo illustrent dramatiquement cette différence de destins. Imagine 1000 investisseurs qui démarrent avec 100 000 € et appliquent différentes stratégies sur 30 ans. Ceux qui utilisent le Kelly complet voient une dispersion énorme des résultats finaux : quelques-uns deviennent milliardaires, mais beaucoup font faillite en cours de route et finissent à zéro. Ceux qui utilisent un demi-Kelly ont des résultats moins spectaculaires au sommet de la distribution, mais presque aucun ne fait faillite. La médiane des résultats est similaire entre les deux groupes, mais la distribution est radicalement différente. Pour un investisseur qui n’a qu’une seule vie et un seul patrimoine à gérer, minimiser le risque de ruine est rationnel même si cela sacrifie les scénarios les plus optimistes. C’est cette sagesse que le critère de Kelly, appliqué avec prudence, permet d’intégrer dans ses décisions.
Un concept connexe et important est celui de l’absorption en théorie des probabilités. Quand tu arrives à zéro, tu es « absorbé » par cet état : il est impossible de remonter sans apport extérieur de capital. Cette irréversibilité de la ruine est ce qui rend la gestion du risque si cruciale. Même avec une stratégie à espérance positive, une série de malchance peut te conduire à l’absorption si tu mises trop gros à chaque tour. Le critère de Kelly, en calibrant précisément la taille des positions, réduit exponentiellement la probabilité d’absorption. Avec un Kelly complet, cette probabilité est faible mais non nulle sur un horizon très long. Avec un fractional Kelly conservateur, elle devient négligeable, proche de zéro. C’est pourquoi les professionnels chevronnés, qui ont vu des collègues se ruiner par excès de confiance, adoptent systématiquement des versions conservatrices de Kelly.
L’effet psychologique de la discipline
Au-delà des mathématiques pures, le critère de Kelly apporte un bénéfice souvent sous-estimé : la discipline psychologique. Avoir une formule objective pour dimensionner ses positions élimine une grande partie du stress émotionnel de l’investissement. Plus besoin de se demander si on mise trop ou pas assez, si on est trop prudent ou trop agressif. La formule donne une réponse, et tu l’appliques méthodiquement. Cette discipline est particulièrement précieuse dans les moments de panique ou d’euphorie des marchés, quand l’émotion pousse à des décisions irrationnelles. Un investisseur qui suit le Kelly calculé restera stable quand les autres paniquent, augmentant mécaniquement ses positions quand les opportunités deviennent plus attractives après une baisse, au lieu de fuir comme le troupeau.
Un autre avantage psychologique majeur est la clarté dans la prise de décision. Le critère de Kelly force à expliciter ses hypothèses : quelle est ma probabilité de gain ? Quel est mon ratio rendement/risque ? Ces questions, une fois posées et répondues honnêtement, révèlent souvent que certaines « opportunités » sont en fait des paris défavorables déguisés en bonnes idées. Combien de fois as-tu acheté une action sur un tuyau de ton beau-frère ou une intuition après avoir lu un article, sans vraiment quantifier tes attentes ? Le processus de calcul du Kelly, même approximatif, oblige à cette réflexion salutaire. Et si tu n’es pas capable d’estimer une probabilité de gain supérieure à 50 %, c’est peut-être le signe que tu ne devrais pas investir du tout dans cette opportunité.
La recherche en finance comportementale confirme l’importance de ces mécanismes de discipline. Les études montrent que les investisseurs qui suivent des règles systématiques surperforment ceux qui décident au cas par cas, même quand les règles sont imparfaites. La raison est que la constance élimine les erreurs comportementales les plus coûteuses : acheter au sommet par euphorie quand tout le monde en parle, vendre au creux par panique quand les médias annoncent la fin du monde, et changer de stratégie au pire moment par impatience. Le critère de Kelly, utilisé comme règle systématique, devient un garde-fou contre ces erreurs. Ce n’est pas une garantie de succès absolu, mais c’est une assurance contre les pires échecs, ceux qui résultent de décisions émotionnelles mal calibrées.
Le psychologue Daniel Kahneman, prix Nobel d’économie pour ses travaux sur les biais cognitifs, a documenté comment les humains sont systématiquement mauvais pour estimer les probabilités et gérer le risque. Nous surestimons les événements rares et spectaculaires, sous-estimons les risques familiers, et sommes victimes de l’effet de disposition (vendre trop tôt les gagnants par peur de perdre les gains, garder trop longtemps les perdants par espoir de récupération). Le critère de Kelly ne corrige pas ces biais directement, mais il dépersonnalise la décision. En remplaçant l’intuition par un calcul, il contourne les circuits émotionnels qui nous font dérailler. Ce n’est pas parfait — tu peux toujours mal estimer les probabilités initiales — mais c’est un progrès significatif vers une gestion plus rationnelle.
Un aspect souvent négligé du bénéfice psychologique du Kelly est la réduction de l’anxiété quotidienne. Les investisseurs qui n’ont pas de cadre clair pour dimensionner leurs positions vivent dans une incertitude permanente : ai-je mis assez ? Ai-je mis trop ? Devrais-je renforcer maintenant que ça baisse ? Devrais-je alléger maintenant que ça monte ? Cette rumination constante consomme de l’énergie mentale et peut conduire à des décisions impulsives prises sur le coup de l’émotion. Avec le critère de Kelly, ces questions ont des réponses calculées à l’avance. Même si les réponses ne sont pas parfaites, le simple fait d’avoir un cadre de décision réduit l’anxiété et libère de la bande passante mentale pour d’autres activités. Les meilleurs investisseurs ne sont pas ceux qui passent le plus de temps à s’inquiéter, mais ceux qui ont des processus clairs qui leur permettent de dormir tranquilles.
Un phénomène bien documenté en psychologie financière est le regret asymétrique. Les gens regrettent davantage les pertes dues à l’action (avoir acheté une action qui a chuté) que les pertes dues à l’inaction (ne pas avoir acheté une action qui a monté). Ce biais pousse naturellement vers l’inaction et le sous-investissement chronique. Le critère de Kelly, en donnant une justification objective à l’action, peut aider à contrebalancer ce biais. Si le Kelly recommande 10 % et que tu mets effectivement 10 %, tu as agi conformément à un cadre rationnel et défendable. Si l’investissement échoue, tu peux te dire que tu as pris une décision raisonnable compte tenu des informations disponibles au moment de la décision. Cette rationalisation post-hoc est plus facile avec un processus documenté qu’avec une intuition floue.
Les limites à ne pas ignorer
Malgré ses qualités indéniables, le critère de Kelly n’est pas une solution miracle, et ses limites doivent être clairement comprises avant de l’appliquer. La première et la plus importante est l’incertitude des paramètres. La formule suppose que tu connais précisément ta probabilité de gain et ton ratio de rendement. Dans la réalité, ces paramètres sont estimés avec une grande incertitude, et une surestimation peut être catastrophique. Si tu penses avoir 60 % de chances de gagner alors qu’en réalité c’est 50 %, le Kelly recommandé sera dangereusement élevé. C’est pourquoi le fractional Kelly est quasi obligatoire en pratique : il intègre une marge de sécurité contre les erreurs d’estimation qui sont inévitables.
La deuxième limite concerne la définition de l’utilité. Le critère de Kelly maximise le taux de croissance logarithmique du capital, ce qui correspond mathématiquement à une fonction d’utilité logarithmique. Mais tous les investisseurs n’ont pas cette fonction d’utilité dans la vie réelle. Certains peuvent avoir des besoins de liquidité à court terme, des objectifs de dépenses fixes à financer, ou une aversion au risque plus forte que la normale. Pour ces investisseurs, le Kelly optimal peut être trop agressif, même en version fractionnelle. Une personne proche de la retraite qui ne peut pas se permettre de voir son portefeuille baisser de 30 % devrait utiliser un Kelly beaucoup plus conservateur qu’un jeune investisseur avec 40 ans devant lui et la capacité de récupérer.
Enfin, le critère de Kelly suppose un horizon temporel infini et la capacité de jouer indéfiniment. Dans la vie réelle, tu as une durée de vie limitée, des besoins de consommation intermédiaires, et tu ne peux pas simplement attendre que la loi des grands nombres fasse son œuvre. Ces contraintes pratiques réduisent l’applicabilité du Kelly pur. La version la plus réaliste pour un investisseur particulier combine plusieurs éléments : un fractional Kelly conservateur (demi-Kelly ou quart-Kelly), une diversification raisonnable pour réduire le risque idiosyncratique, et une allocation d’actifs globale qui tient compte de l’âge et des objectifs de vie. Le critère de Kelly devient alors un outil parmi d’autres dans la boîte à outils, plutôt qu’une règle absolue à suivre aveuglément.
Une limite supplémentaire, souvent négligée par les théoriciens, est l’hypothèse de marchés liquides et sans coûts de transaction. Le critère de Kelly recommande de rééquilibrer continuellement le portefeuille pour maintenir les proportions optimales. En pratique, chaque transaction génère des frais (commissions de courtage, spread bid-ask, impact de marché pour les gros ordres) et potentiellement des impôts sur les plus-values réalisées. Ces coûts érodent le rendement et peuvent rendre le rééquilibrage fréquent contre-productif voire destructeur de valeur. Un investisseur avisé appliquera le Kelly avec une bande de tolérance : ne rééquilibrer que lorsque l’écart par rapport à l’allocation cible dépasse un certain seuil, par exemple 5 ou 10 points de pourcentage, plutôt qu’à chaque petit mouvement du marché.
🛠️ Comment l’utiliser dès demain (sans être matheux)
Étape 1 : Estimer ton avantage
La première étape pour appliquer le critère de Kelly est d’estimer honnêtement ton avantage sur chaque investissement potentiel. Cette étape est la plus difficile car elle demande une lucidité et une humilité que peu d’investisseurs possèdent naturellement. Commence par te poser une question simple et brutale : qu’est-ce que je sais que le marché ne sait pas ? Si la réponse est « rien de significatif », alors tu n’as aucun avantage et le Kelly recommande de ne pas investir activement, mais de te contenter d’un ETF diversifié qui capte le rendement moyen du marché. Ce n’est pas une insulte, c’est une réalité statistique : la majorité des investisseurs professionnels avec des équipes d’analystes n’arrivent pas à battre le marché sur le long terme après frais. Si tu n’as pas d’avantage particulier, l’investissement passif est mathématiquement optimal.
Si tu penses avoir un avantage, quantifie-le de manière conservative, pas optimiste. Imaginons que tu suives une entreprise depuis des années parce que tu travailles dans son secteur, que tu comprennes son marché mieux que la plupart des analystes financiers, et que tu penses qu’elle est sous-évaluée de 30 % par rapport à sa valeur intrinsèque. Quelle est ta probabilité d’avoir raison ? Pas 100 %, certainement. Même pas 90 %. Avec une grande honnêteté, peut-être 60 à 70 % si ton analyse est vraiment solide. Et si tu as raison, quel sera le rendement réalisé ? Pas forcément les 30 % de sous-évaluation, car le marché peut rester irrationnel longtemps, parfois des années. Peut-être 15 à 20 % sur deux ans si tout va bien. Avec ces paramètres conservateurs, le critère de Kelly te donnera une taille de position raisonnable. L’erreur classique est de surestimer sa confiance et le rendement espéré, conduisant à des positions surdimensionnées.
Une technique utile pour calibrer tes estimations est le pré-mortem, développé par le psychologue Gary Klein. Avant d’investir, imagine que tu es dans un an et que ton investissement a échoué lamentablement. Quelles sont les raisons plausibles de cet échec ? Le marché s’est retourné ? La concurrence a lancé un produit supérieur ? Le management a fait des erreurs stratégiques ? Les régulateurs ont durci les règles ? Cette liste de risques te permet d’ajuster ta probabilité de succès à la baisse. Si tu trouves cinq raisons crédibles pour lesquelles ça pourrait mal tourner, peut-être que ta confiance de 70 % devrait être ramenée à 55 %. Le pré-mortem est un antidote puissant contre l’excès de confiance, le biais cognitif le plus dangereux pour un investisseur.
Une autre approche complémentaire est de comparer avec des cas similaires passés, ce que les psychologues appellent l’« outside view ». Si tu penses qu’une biotech a 70 % de chances de voir son médicament approuvé par la FDA, compare cette estimation aux taux d’approbation historiques de la FDA pour ce type de médicament à ce stade de développement. Si le taux historique est de 40 %, ta confiance de 70 % est probablement injustifiée, à moins d’avoir une information spécifique et vérifiable que le marché ignore. Cette méthode de calibration par référence extérieure est recommandée par les meilleurs prévisionnistes professionnels. Elle contrebalance la tendance naturelle à surestimer ses propres analyses (inside view) et produit des estimations plus réalistes pour alimenter le calcul de Kelly.
Étape 2 : Calculer la fraction de Kelly
Une fois tes paramètres estimés avec prudence, le calcul lui-même est trivial. Rappelle-toi la formule de base : **f* = (bp - q) / b**, où p est ta probabilité de gain, q = 1 - p ta probabilité de perte, et b le ratio entre ce que tu gagnes et ce que tu perds. Prenons un exemple concret pour bien fixer les idées. Tu penses avoir 60 % de chances de gagner 25 % et 40 % de chances de perdre 15 % si tu te trompes. Tes paramètres sont : p = 0,6, q = 0,4, et b = 25/15 = 1,67 (tu gagnes 1,67 fois ce que tu risques, puisque le gain potentiel est plus grand que la perte potentielle). Le Kelly est donc f* = (1,67 × 0,6 - 0,4) / 1,67 = (1 - 0,4) / 1,67 = 0,6 / 1,67 = 36 %. En Kelly complet, tu devrais allouer 36 % de ton portefeuille à cette position.
En pratique, tu vas diviser ce résultat par deux ou plus pour obtenir ton fractional Kelly. Avec un demi-Kelly, la position serait de 18 %. Avec un quart-Kelly, 9 %. Le choix entre ces options dépend de ta confiance dans tes estimations et de ta tolérance à la volatilité. Si tu es nouveau dans ce type d’analyse probabiliste, commence avec un quart-Kelly. Si tu as un historique prouvé de bonnes estimations sur plusieurs années, tu peux monter à un demi-Kelly. Très peu d’investisseurs devraient utiliser plus d’un demi-Kelly, sauf dans des cas exceptionnels où l’avantage est quasi certain (ce qui est extrêmement rare sur les marchés efficients).
Pour les situations plus complexes avec plusieurs résultats possibles, tu peux utiliser la version simplifiée basée sur le ratio de Sharpe espéré. Estime le rendement espéré (disons 12 % par an au-delà du taux sans risque) et la volatilité attendue (disons 30 % par an). Le Kelly approximatif est rendement / volatilité² = 12 % / 9 % = 1,33, soit 133 % du portefeuille. Évidemment, c’est irréaliste sans levier financier, donc tu plafonnes à 100 %. Avec un demi-Kelly, ce serait 50 % maximum. Cette méthode est moins précise que la formule originale pour les paris binaires, mais elle est applicable à n’importe quel actif dont tu peux estimer le rendement et la volatilité espérés.
Un outil pratique pour ne pas se tromper est de créer un tableau Excel simple qui calcule automatiquement le Kelly pour différents scénarios. Les colonnes seraient : probabilité de gain, gain potentiel en pourcentage, perte potentielle en pourcentage, Kelly complet calculé, demi-Kelly, quart-Kelly. En remplissant ce tableau avant chaque investissement, tu forces ta réflexion dans un cadre rigoureux et tu évites les calculs de coin de table qui peuvent être sources d’erreurs. Ce tableau peut aussi servir de journal de bord : en notant tes estimations et les résultats réels, tu pourras mesurer la qualité de ton calibrage au fil du temps et t’améliorer progressivement.
Étape 3 : Gérer le portefeuille global
Le critère de Kelly s’applique idéalement à chaque position individuellement, mais la vraie difficulté pratique est de gérer l’ensemble du portefeuille de manière cohérente. Si tu as dix idées d’investissement, chacune avec son propre Kelly calculé, la somme peut facilement dépasser 100 %. C’est là que la corrélation entre les positions devient cruciale et ne peut être ignorée. Des positions corrélées (par exemple, plusieurs actions tech exposées aux mêmes facteurs) doivent être traitées comme un seul bloc pour le calcul du Kelly global. Une règle pratique est de limiter l’exposition totale aux actifs risqués à 60-80 % du portefeuille, en gardant le reste en liquidités ou en actifs très sûrs. Cette réserve te permet de saisir de nouvelles opportunités quand elles se présentent et de survivre aux crises sans être forcé de vendre.
Une approche structurée consiste à hiérarchiser tes opportunités par ratio Kelly/risque ou par niveau de conviction. Place en premier les positions où ton avantage est le plus clair et le plus robuste, celles où tu as vraiment fait tes devoirs. Ensuite, ajoute les positions secondaires jusqu’à atteindre ton allocation cible en actifs risqués. Les positions les moins certaines peuvent être réduites ou éliminées si le portefeuille est déjà bien garni. Cette discipline évite le piège classique de l’investisseur qui accumule des positions médiocres « au cas où » ou « pour diversifier », diluant son capital entre trop d’idées moyennes plutôt que de le concentrer sur les meilleures.
Enfin, le rééquilibrage périodique est essentiel pour maintenir les proportions Kelly au fil du temps. Quand une position gagne beaucoup, sa part du portefeuille augmente mécaniquement, ce qui la rend potentiellement surdimensionnée par rapport au Kelly optimal actuel. Inversement, une position qui baisse peut devenir sous-dimensionnée et mériter un renforcement si la thèse d’investissement reste valide. Le rééquilibrage trimestriel ou semestriel, combiné avec une réévaluation des paramètres Kelly, permet de maintenir un portefeuille aligné avec tes convictions actuelles. Ce processus discipliné est aussi important que le calcul initial, car les marchés évoluent et tes estimations doivent évoluer avec eux.
Pour les investisseurs qui gèrent un portefeuille diversifié, une approche en couches peut être utile et structurante. La première couche est le cœur passif (ETF monde, par exemple), dimensionné selon ta tolérance au risque globale et ton horizon temporel. La deuxième couche est constituée de paris sectoriels ou thématiques où tu penses avoir un avantage modéré, dimensionnés à 50-100 % du Kelly calculé. La troisième couche est constituée de positions de conviction forte sur des entreprises individuelles, dimensionnées à 25-50 % du Kelly. Cette structure permet de bénéficier de la diversification du cœur tout en capturant l’alpha potentiel des positions satellites, le tout dans un cadre de risque maîtrisé et cohérent.
Étape 4 : Suivre et ajuster
L’application du critère de Kelly n’est pas un événement ponctuel mais un processus continu d’apprentissage et d’amélioration. Après chaque investissement, note tes estimations initiales (probabilité de gain, ratio de rendement) et compare-les aux résultats réels quand la position est clôturée. Au fil du temps, cette pratique révélera tes biais systématiques que tu ignores peut-être. Peut-être surestime-tu régulièrement tes probabilités de succès de 10 points parce que tu es naturellement optimiste. Peut-être sous-estimes-tu la volatilité des actions small cap parce que tu n’as pas vécu de krach majeur. Ces insights te permettent d’ajuster tes estimations futures et d’améliorer progressivement la qualité de ton Kelly.
Un journal d’investissement est l’outil idéal pour ce suivi rigoureux. Pour chaque position, enregistre la date d’achat, le montant investi, la fraction Kelly calculée, les hypothèses utilisées (probabilité, rendements), et tes raisons qualitatives pour cet investissement. À la clôture de la position, ajoute le résultat réel et une analyse post-mortem : qu’est-ce qui s’est passé comme prévu ? Qu’est-ce qui a surpris ? Aurais-tu dû voir venir ce qui est arrivé ? Après quelques années, ce journal devient une mine d’or de données sur ta propre performance et tes tendances comportementales. Les investisseurs qui tiennent ce type de journal surperforment systématiquement ceux qui n’en tiennent pas, car ils apprennent de leurs erreurs au lieu de les répéter.
Le critère de Kelly, en fin de compte, est autant un cadre de réflexion qu’une formule mathématique à appliquer mécaniquement. Il t’oblige à penser en termes de probabilités et de risque asymétrique. Il te rappelle que la taille de position est une décision cruciale, pas un détail secondaire. Il te protège contre les excès émotionnels en fournissant un ancrage objectif. Même si tu ne calcules jamais un Kelly exact avec trois décimales, intégrer ces principes dans ta pensée d’investisseur te rendra plus discipliné, plus rationnel, et probablement plus performant sur le long terme. C’est peut-être là le vrai cadeau de John Kelly : non pas une formule magique qui garantit la richesse, mais une façon de penser le risque qui transforme l’amateurisme en professionnalisme.
Pour aller plus loin dans ta compréhension, plusieurs ressources approfondissent le sujet de manière accessible. Le livre « A Man for All Markets » d’Edward Thorp raconte son parcours fascinant des casinos à Wall Street et explique comment il a appliqué le critère de Kelly dans la pratique pendant des décennies. « Fortune’s Formula » de William Poundstone retrace l’histoire captivante de la formule et de ses protagonistes colorés. Et pour les plus mathématiciens, l’article original de Kelly de 1956, disponible gratuitement en ligne, reste étonnamment lisible et pertinent soixante-dix ans plus tard. Ces lectures te donneront une compréhension encore plus profonde de ce qui est probablement l’outil de gestion du risque le plus puissant jamais développé.
Une erreur fréquente des débutants est de sur-compliquer le Kelly en essayant d’intégrer trop de paramètres sophistiqués. La beauté de la formule originale réside dans sa simplicité : probabilité de gain, ratio de gain, point final. Les versions sophistiquées avec distributions continues, corrélations multi-actifs, et ajustements dynamiques sont intellectuellement élégantes et publiables dans des revues académiques, mais elles introduisent aussi plus d’opportunités d’erreurs de calcul ou d’estimation. Pour la plupart des investisseurs particuliers, un Kelly simple avec des estimations conservatrices sera plus robuste qu’un modèle complexe avec des estimations incertaines. Comme disait Einstein, « tout devrait être aussi simple que possible, mais pas plus simple ». Le Kelly simple est souvent le niveau optimal de complexité.
Un dernier conseil pratique : teste le Kelly sur papier avant de l’appliquer avec de l’argent réel. Pendant quelques mois, calcule le Kelly pour chaque opportunité d’investissement que tu envisages, note la taille de position recommandée, mais n’agis pas encore avec ton vrai capital. Compare ensuite les résultats théoriques de ton portefeuille Kelly avec les résultats de tes décisions réelles. Cette expérience te permettra de développer ton intuition pour les calculs de probabilités, d’identifier tes biais d’estimation, et de gagner confiance dans la méthode avant de l’utiliser en conditions réelles avec des enjeux financiers. C’est l’équivalent des simulations de vol pour les pilotes : un environnement sûr pour apprendre sans les conséquences catastrophiques des erreurs.
🎯 À toi de jouer (mais bien)
Le critère de Kelly répond à une question que la plupart des investisseurs évitent soigneusement : combien investir exactement dans chaque opportunité ? La réponse, contrairement aux règles empiriques habituelles tirées de livres de développement personnel, est fondée sur des mathématiques solides développées il y a plus de soixante ans. La formule dit que la taille optimale de ta position dépend de deux facteurs principaux : ton avantage (la différence entre ta probabilité de gain et ce que les cotes impliquent) et le ratio entre ce que tu peux gagner et ce que tu peux perdre. Plus ton avantage est grand et plus le risque de perte est faible par rapport au gain potentiel, plus tu peux miser gros. Simple en théorie, puissant en pratique quand appliqué avec discipline.
La leçon la plus importante du critère de Kelly n’est pas la formule elle-même, mais la discipline qu’elle impose dans ta réflexion. Estimer explicitement tes probabilités de gain te force à justifier tes investissements avec des arguments concrets. Calculer le ratio rendement/risque te rappelle que le gain potentiel n’est pas le seul facteur à considérer. Utiliser un fractional Kelly te protège contre ta propre confiance excessive qui est le piège de tout investisseur. Et suivre tes résultats au fil du temps te permet d’apprendre et de t’améliorer continuellement. Ces pratiques, bien plus que n’importe quelle formule magique, sont ce qui distingue les investisseurs qui réussissent de ceux qui échouent sur le long terme.
Pour mettre en pratique ce que tu viens d’apprendre, commence petit et progresse graduellement. Choisis une position de ton portefeuille actuel et essaie d’estimer sa probabilité de gain et son ratio rendement/risque avec honnêteté. Calcule le Kelly correspondant et compare-le à la taille réelle de ta position. Es-tu surdimensionné par rapport à ce que la formule recommande ? Sous-dimensionné ? Cette simple comparaison peut révéler des surprises et des incohérences dans ta gestion actuelle. Ensuite, applique le même processus à tes nouvelles décisions d’investissement. Avec le temps, ce cadre de réflexion deviendra naturel, et tes décisions seront plus cohérentes et mieux calibrées.
Une dernière réflexion pour conclure cette exploration. Le critère de Kelly a été développé par un physicien brillant, popularisé par un compteur de cartes devenu milliardaire, adopté par des hedge funds légendaires, et reste pourtant méconnu du grand public et même de beaucoup de professionnels de la finance. Cette obscurité relative est peut-être une bénédiction déguisée pour ceux qui font l’effort de le comprendre. Comme le disait Charlie Munger avec son humour caractéristique, « si investir était facile, tout le monde serait riche ». Le critère de Kelly n’est pas facile à appliquer correctement — il demande rigueur intellectuelle, honnêteté avec soi-même, et discipline émotionnelle dans l’exécution. Mais c’est précisément cette difficulté qui en fait un avantage compétitif pour ceux qui font l’effort de le maîtriser. Tu fais maintenant partie de ceux qui connaissent la formule. La question est : vas-tu l’utiliser ?
Si tu devais retenir seulement trois choses de cette newsletter, ce seraient celles-ci. Premièrement, la taille de position n’est pas un détail mais une décision fondamentale qui peut faire la différence entre la richesse et la ruine sur le long terme. La meilleure idée d’investissement du monde, mal exécutée en termes de position sizing, peut te laisser plus pauvre qu’un investisseur médiocre avec une bonne discipline. Deuxièmement, l’intuition est ton ennemie dans ce domaine. Les humains sont câblés pour mal évaluer les probabilités et les risques, et seul un cadre quantitatif comme le critère de Kelly peut te protéger contre ces biais cognitifs profondément ancrés. Troisièmement, la prudence est mathématiquement justifiée. Le fractional Kelly (demi-Kelly ou quart-Kelly) est presque toujours préférable au Kelly complet, car les conséquences de surmiser sont bien pires que celles de sous-miser. Dans le doute, mise moins.
Le critère de Kelly ne garantit pas le succès — aucune formule ne le peut sur des marchés incertains par nature. Mais il te donne les outils pour maximiser tes chances sur le long terme, en évitant les erreurs les plus coûteuses que commettent la majorité des investisseurs. C’est un compagnon de route précieux dans un voyage qui durera des décennies, et son influence sur ta pensée d’investisseur dépassera de loin les simples calculs de pourcentages. Le vrai cadeau de John Kelly n’est pas une formule, c’est une façon de voir le monde : en termes de probabilités, de risques, et de décisions optimales face à l’incertitude. Cette perspective, une fois acquise, ne te quittera plus jamais.
Pour terminer sur une note pratique, voici un résumé des règles d’or du critère de Kelly que tu peux afficher près de ton écran quand tu prends des décisions d’investissement. Règle numéro un : estime toujours explicitement ta probabilité de gain et ton ratio rendement/risque avant d’investir, même approximativement. Règle numéro deux : utilise systématiquement un fractional Kelly (demi-Kelly ou quart-Kelly) plutôt que le Kelly complet, pour te protéger contre tes erreurs d’estimation. Règle numéro trois : traite les positions corrélées comme un bloc unique et limite ton exposition totale aux actifs risqués à 60-80 % du portefeuille. Règle numéro quatre : tiens un journal de tes estimations et de tes résultats pour améliorer ton calibrage au fil du temps. Règle numéro cinq : ne suis jamais la formule aveuglément, mais utilise-la comme un cadre de réflexion pour discipliner ta pensée.
Ces cinq règles, appliquées avec constance sur des années et des décennies, te mettront dans une position bien meilleure que la grande majorité des investisseurs qui naviguent au feeling, au tuyau, et à l’émotion du moment. Le critère de Kelly n’est pas une baguette magique, mais c’est l’outil le plus proche d’une baguette magique que les mathématiques nous aient donné pour la gestion du risque. John Kelly serait fier de savoir que sa formule, conçue initialement pour optimiser les transmissions téléphoniques, aide aujourd’hui des millions d’investisseurs à prendre de meilleures décisions financières. À toi maintenant de l’utiliser.
Vous voulez aller plus loin ?
Je peux répondre aux questions que vous vous posez via Wathsapp, je lance ce service sans frais afin que vous ayez accès à du conseil en finances personnelles en toute simplicité. Le lien : https://wa.me/33613018211
Disclaimer : Ceci n’est pas un conseil en investissement, en tant que CIF, je ne peux donner de conseils avant d’avoir pu comprendre qui vous êtes, vos objectifs de vie, vos contraintes et capacités financières. Tout conseil étant personnalisé, et cette newsletter étant généraliste, soyez vigilant sur vos investissements, peu importe la forme qu’ils prendraient.